'vector' Dialect
MLIR supports multi-dimensional vector types and custom operations on those
types. A generic, retargetable, higher-order vector type (n-D with n > 1)
is a structured type, that carries semantic information useful for
transformations. This document discusses retargetable abstractions that exist in
MLIR today and operate on ssa-values of type vector along with pattern
rewrites and lowerings that enable targeting specific instructions on concrete
targets. These abstractions serve to separate concerns between operations on
memref (a.k.a buffers) and operations on vector values. This is not a new
proposal but rather a textual documentation of existing MLIR components along
with a rationale.
Positioning in the Codegen Infrastructure ¶
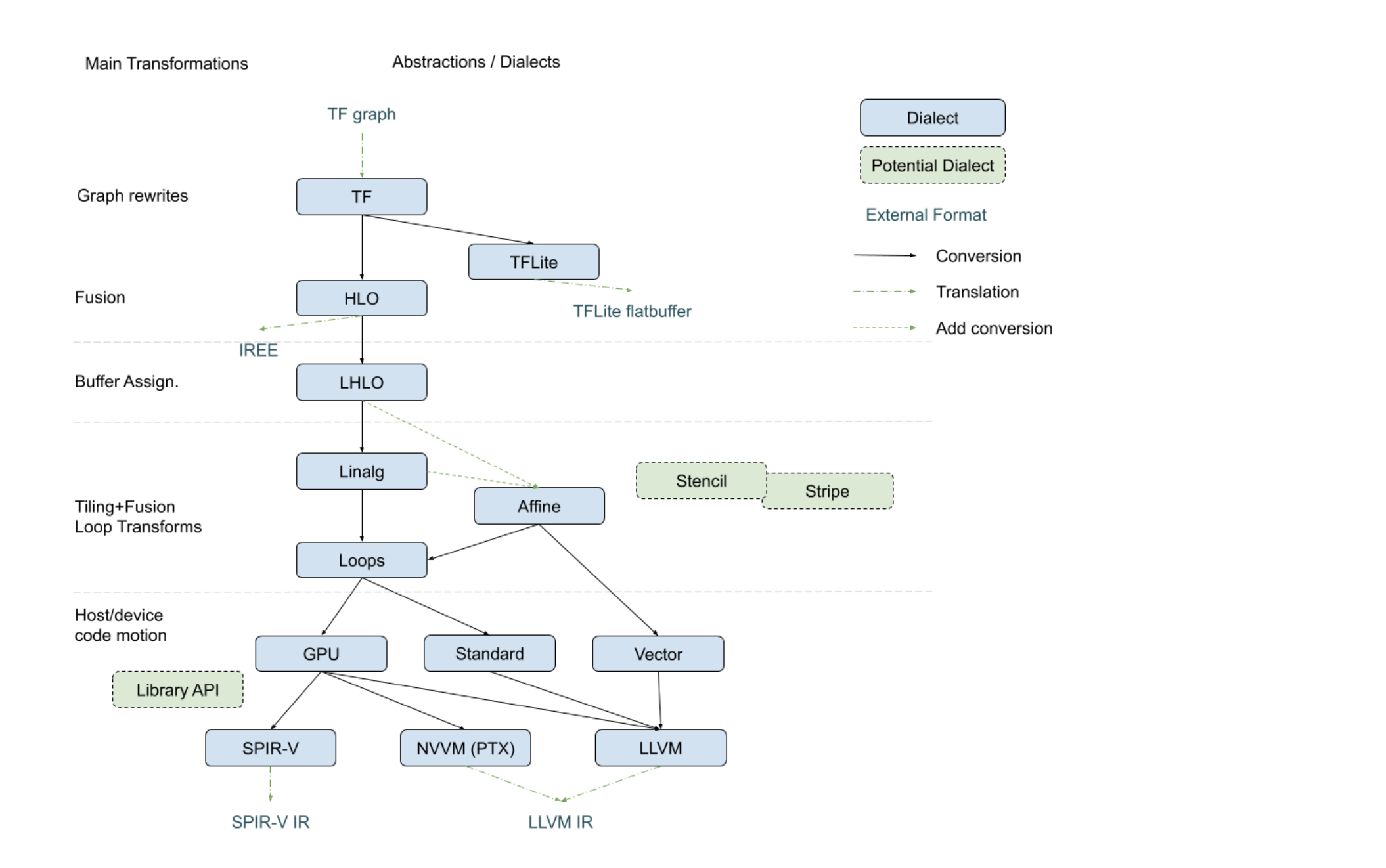
The following diagram, recently presented with the
StructuredOps abstractions,
captures the current codegen paths implemented in MLIR in the various existing
lowering paths.
The following diagram seeks to isolate vector dialects from the complexity of
the codegen paths and focus on the payload-carrying ops that operate on std and
vector types. This diagram is not to be taken as set in stone and
representative of what exists today but rather illustrates the layering of
abstractions in MLIR.

This separates concerns related to (a) defining efficient operations on
vector types from (b) program analyses + transformations on memref, loops
and other types of structured ops (be they HLO, LHLO, Linalg or other ).
Looking a bit forward in time, we can put a stake in the ground and venture that
the higher level of vector-level primitives we build and target from codegen
(or some user/language level), the simpler our task will be, the more complex
patterns can be expressed and the better performance will be.
Components of a Generic Retargetable Vector-Level Dialect ¶
The existing MLIR vector-level dialects are related to the following bottom-up
abstractions:
- Representation in
LLVMIRvia data structures, instructions and intrinsics. This is referred to as theLLVMlevel. - Set of machine-specific operations and types that are built to translate
almost 1-1 with the HW ISA. This is referred to as the Hardware Vector
level; a.k.a
HWV. For instance, we have (a) theNVVMdialect (forCUDA) with tensor core ops, (b) accelerator-specific dialects (internal), a potential (future)CPUdialect to captureLLVMintrinsics more closely and other dialects for specific hardware. Ideally this should be auto-generated as much as possible from theLLVMlevel. - Set of virtual, machine-agnostic, operations that are informed by costs at
the
HWV-level. This is referred to as the Virtual Vector level; a.k.aVV. This is the level that higher-level abstractions (codegen, automatic vectorization, potential vector language, …) targets.
The existing generic, retargetable, vector-level dialect is related to the
following top-down rewrites and conversions:
- MLIR Rewrite Patterns applied by the MLIR
PatternRewriteinfrastructure to progressively lower to implementations that match closer and closer to theHWV. Some patterns are “in-dialect”VV -> VVand some are conversionsVV -> HWV. Virtual Vector -> Hardware Vectorlowering is specified as a set of MLIR lowering patterns that are specified manually for now.Hardware Vector -> LLVMlowering is a mechanical process that is written manually at the moment and that should be automated, following theLLVM -> Hardware Vectorops generation as closely as possible.
Short Description of the Existing Infrastructure ¶
LLVM level ¶
On CPU, the n-D vector type currently lowers to !llvm<array<vector>>. More
concretely, vector<4x8x128xf32> lowers to !llvm<[4 x [ 8 x [ 128 x float ]]]>. There are tradeoffs involved related to how one can access subvectors and
how one uses llvm.extractelement, llvm.insertelement and
llvm.shufflevector. A
deeper dive section discusses the current
lowering choices and tradeoffs.
Hardware Vector Ops ¶
Hardware Vector Ops are implemented as one dialect per target. For internal
hardware, we are auto-generating the specific HW dialects. For GPU, the NVVM
dialect adds operations such as mma.sync, shfl and tests. For CPU things
are somewhat in-flight because the abstraction is close to LLVMIR. The jury is
still out on whether a generic CPU dialect is concretely needed, but it seems
reasonable to have the same levels of abstraction for all targets and perform
cost-based lowering decisions in MLIR even for LLVM. Specialized CPU
dialects that would capture specific features not well captured by LLVM peephole
optimizations of on different types that core MLIR supports (e.g. Scalable
Vectors) are welcome future extensions.
Virtual Vector Ops ¶
Some existing Arith and Vector Dialect on n-D vector types comprise:
// Produces a vector<3x7x8xf32>
%a = arith.addf %0, %1 : vector<3x7x8xf32>
// Produces a vector<3x7x8xf32>
%b = arith.mulf %0, %1 : vector<3x7x8xf32>
// Produces a vector<3x7x8xf32>
%c = vector.splat %1 : vector<3x7x8xf32>
%d = vector.extract %0[1]: vector<7x8xf32> from vector<3x7x8xf32>
%e = vector.extract %0[1, 5]: vector<8xf32> from vector<3x7x8xf32>
%f = vector.outerproduct %0, %1: vector<4xf32>, vector<8xf32> // -> vector<4x8xf32>
%g = vector.outerproduct %0, %1, %2: vector<4xf32>, vector<8xf32> // fma when adding %2
// Returns a slice of type vector<2x2x16xf32>
%h = vector.strided_slice %0
{offsets = [2, 2], sizes = [2, 2], strides = [1, 1]}:
vector<4x8x16xf32>
%i = vector.transfer_read %A[%0, %1]
{permutation_map = (d0, d1) -> (d0)}:
memref<7x?xf32>, vector<4xf32>
vector.transfer_write %f1, %A[%i0, %i1, %i2, %i3]
{permutation_map = (d0, d1, d2, d3) -> (d3, d1, d0)} :
vector<5x4x3xf32>, memref<?x?x?x?xf32>
The list of Vector is currently undergoing evolutions and is best kept track of
by following the evolution of the
VectorOps.td
ODS file (markdown documentation is automatically generated locally when
building and populates the
Vector doc).
Recent extensions are driven by concrete use cases of interest. A notable such
use case is the vector.contract op which applies principles of the
StructuredOps abstraction to vector types.
Virtual Vector Rewrite Patterns ¶
The following rewrite patterns exist at the VV->VV level:
- The now retired
MaterializeVectorpass used to legalize ops on a coarse-grained virtualvectorto a finer-grained virtualvectorby unrolling. This has been rewritten as a retargetable unroll-and-jam pattern onvectorops andvectortypes. - The lowering of
vector_transferops legalizesvectorload/store ops to permuted loops over scalar load/stores. This should evolve to loops overvectorload/stores +maskoperations as they become availablevectorops at theVVlevel.
The general direction is to add more Virtual Vector level ops and implement more
useful VV -> VV rewrites as composable patterns that the PatternRewrite
infrastructure can apply iteratively.
Virtual Vector to Hardware Vector Lowering ¶
For now, VV -> HWV are specified in C++ (see for instance the
SplatOpLowering for n-D vectors
or the
VectorOuterProductOp lowering).
Simple
conversion tests
are available for the LLVM target starting from the Virtual Vector Level.
Rationale ¶
Hardware as vector Machines of Minimum Granularity ¶
Higher-dimensional vectors are ubiquitous in modern HPC hardware. One way to
think about Generic Retargetable vector-Level Dialect is that it operates on
vector types that are multiples of a “good” vector size so the HW can
efficiently implement a set of high-level primitives (e.g.
vector<8x8x8x16xf32> when HW vector size is say vector<4x8xf32>).
Some notable vector sizes of interest include:
- CPU:
vector<HW_vector_size * k>,vector<core_count * k’ x HW_vector_size * k>andvector<socket_count x core_count * k’ x HW_vector_size * k> - GPU:
vector<warp_size * k>,vector<warp_size * k x float4>andvector<warp_size * k x 4 x 4 x 4>for tensor_core sizes, - Other accelerators: n-D
vectoras first-class citizens in the HW.
Depending on the target, ops on sizes that are not multiples of the HW vector
size may either produce slow code (e.g. by going through LLVM legalization) or
may not legalize at all (e.g. some unsupported accelerator X combination of ops
and types).
Transformations Problems Avoided ¶
A vector<16x32x64xf32> virtual vector is a coarse-grained type that can be
“unrolled” to HW-specific sizes. The multi-dimensional unrolling factors are
carried in the IR by the vector type. After unrolling, traditional
instruction-level scheduling can be run.
The following key transformations (along with the supporting analyses and
structural constraints) are completely avoided by operating on a vector
ssa-value abstraction:
- Loop unroll and unroll-and-jam.
- Loop and load-store restructuring for register reuse.
- Load to store forwarding and Mem2reg.
- Coarsening (raising) from finer-grained
vectorform.
Note that “unrolling” in the context of vectors corresponds to partial loop
unroll-and-jam and not full unrolling. As a consequence this is expected to
compose with SW pipelining where applicable and does not result in ICache blow
up.
The Big Out-Of-Scope Piece: Automatic Vectorization ¶
One important piece not discussed here is automatic vectorization (automatically
raising from scalar to n-D vector ops and types). The TL;DR is that when the
first “super-vectorization” prototype was implemented, MLIR was nowhere near as
mature as it is today. As we continue building more abstractions in VV -> HWV,
there is an opportunity to revisit vectorization in MLIR.
Since this topic touches on codegen abstractions, it is technically out of the
scope of this survey document but there is a lot to discuss in light of
structured op type representations and how a vectorization transformation can be
reused across dialects. In particular, MLIR allows the definition of dialects at
arbitrary levels of granularity and lends itself favorably to progressive
lowering. The argument can be made that automatic vectorization on a loops + ops
abstraction is akin to raising structural information that has been lost.
Instead, it is possible to revisit vectorization as simple pattern rewrites,
provided the IR is in a suitable form. For instance, vectorizing a
linalg.generic op whose semantics match a matmul can be done
quite easily with a pattern.
In fact this pattern is trivial to generalize to any type of contraction when
targeting the vector.contract op, as well as to any field (+/*, min/+,
max/+, or/and, logsumexp/+ …) . In other words, by operating on a higher
level of generic abstractions than affine loops, non-trivial transformations
become significantly simpler and composable at a finer granularity.
Irrespective of the existence of an auto-vectorizer, one can build a notional
vector language based on the VectorOps dialect and build end-to-end models with
expressing vectors in the IR directly and simple pattern-rewrites.
EDSCs
provide a simple way of driving such a notional language directly in C++.
Bikeshed Naming Discussion ¶
There are arguments against naming an n-D level of abstraction vector because
most people associate it with 1-D vectors. On the other hand, vectors are
first-class n-D values in MLIR. The alternative name Tile has been proposed,
which conveys higher-D meaning. But it also is one of the most overloaded terms
in compilers and hardware. For now, we generally use the n-D vector name and
are open to better suggestions.
0D Vectors ¶
Vectors of dimension 0 (or 0-D vectors or 0D vectors) are allowed inside
MLIR. For instance, a f32 vector containing one scalar can be denoted as
vector<f32>. This is similar to the tensor<f32> type that is available in
TensorFlow or the memref<f32> type that is available in MLIR.
Generally, a 0D vector can be interpreted as a scalar. The benefit of 0D
vectors, tensors, and memrefs is that they make it easier to lower code
from various frontends such as TensorFlow and make it easier to handle corner
cases such as unrolling a loop from 1D to 0D.
LLVM Lowering Tradeoffs ¶
This section describes the tradeoffs involved in lowering the MLIR n-D vector type and operations on it to LLVM-IR. Putting aside the LLVM Matrix proposal for now, this assumes LLVM only has built-in support for 1-D vector. The relationship with the LLVM Matrix proposal is discussed at the end of this document.
MLIR does not currently support dynamic vector sizes (i.e. SVE style) so the
discussion is limited to static rank and static vector sizes (e.g.
vector<4x8x16x32xf32>). This section discusses operations on vectors in LLVM
and MLIR.
LLVM instructions are prefixed by the llvm. dialect prefix (e.g.
llvm.insertvalue). Such ops operate exclusively on 1-D vectors and aggregates
following the
LLVM LangRef. MLIR
operations are prefixed by the vector. dialect prefix (e.g.
vector.insertelement). Such ops operate exclusively on MLIR n-D vector
types.
Alternatives For Lowering an n-D Vector Type to LLVM ¶
Consider a vector of rank n with static sizes {s_0, ... s_{n-1}} (i.e. an MLIR
vector<s_0x...s_{n-1}xf32>). Lowering such an n-D MLIR vector type to an
LLVM descriptor can be done by either:
- Flattening to a
1-Dvector:!llvm<"(s_0*...*s_{n-1})xfloat">in the MLIR LLVM dialect. - Nested aggregate type of
1-Dvector:!llvm."[s_0x[s_1x[...<s_{n-1}xf32>]]]">in the MLIR LLVM dialect. - A mix of both.
There are multiple tradeoffs involved in choosing one or the other that we
discuss. It is important to note that “a mix of both” immediately reduces to
“nested aggregate type of 1-D vector” with a vector.cast %0: vector<4x8x16x32xf32> to vector<4x4096xf32> operation, that flattens the most
“k” minor dimensions.
Constraints Inherited from LLVM (see LangRef) ¶
The first constraint was already mentioned: LLVM only supports 1-D vector
types natively. Additional constraints are related to the difference in LLVM
between vector and aggregate types: “Aggregate Types are a subset of derived types that can contain multiple member types. Arrays and structs are aggregate types. Vectors are not considered to be aggregate types.”.
This distinction is also reflected in some of the operations. For 1-D vectors,
the operations llvm.extractelement, llvm.insertelement, and
llvm.shufflevector apply, with direct support for dynamic indices. For n-D
vectors with n>1, and thus aggregate types at LLVM level, the more restrictive
operations llvm.extractvalue and llvm.insertvalue apply, which only accept
static indices. There is no direct shuffling support for aggregate types.
The next sentence illustrates a recurrent tradeoff, also found in MLIR, between
“value types” (subject to SSA use-def chains) and “memory types” (subject to
aliasing and side-effects): “Structures in memory are accessed using ‘load’ and ‘store’ by getting a pointer to a field with the llvm.getelementptr instruction. Structures in registers are accessed using the llvm.extractvalue and llvm.insertvalue instructions.”
When transposing this to MLIR, llvm.getelementptr works on pointers to n-D
vectors in memory. For n-D, vectors values that live in registers we can use
vector.extract and vector.insert which do not accept dynamic indices. Note
that this is consistent with hardware considerations as discussed below.
An alternative is to use an LLVM 1-D vector type for which one can use
llvm.extractelement, llvm.insertelement and llvm.shufflevector. These
operations accept dynamic indices. The implication is that one has to use a
flattened lowering of an MLIR n-D vector to an LLVM 1-D vector.
There are multiple tradeoffs involved that mix implications on the programming model, execution on actual HW and what is visible or hidden from codegen. They are discussed in the following sections.
Nested Aggregate ¶
Pros:
- Natural encoding n-D vector -> (n-1)-D aggregate over 1-D vector.
- No need for linearization / delinearization logic inserted everywhere.
llvm.insertvalue,llvm.extractvalueof(n-k)-Daggregate is natural.llvm.insertelement,llvm.extractelement,llvm.shufflevectorover1-Dvector type is natural.
Cons:
llvm.insertvalue/llvm.extractvaluedoes not accept dynamic indices but only static ones.- Dynamic indexing on the non-most-minor dimension requires roundtrips to memory.
- Special intrinsics and native instructions in LLVM operate on
1-Dvectors. This is not expected to be a practical limitation thanks to avector.cast %0: vector<4x8x16x32xf32> to vector<4x4096xf32>operation, that flattens the most minor dimensions (see the bigger picture in implications on codegen).
Flattened 1-D Vector Type ¶
Pros:
insertelement/extractelement/shufflevectorwith dynamic indexing is possible over the whole loweredn-Dvector type.- Supports special intrinsics and native operations.
Cons:
- Requires linearization/delinearization logic everywhere, translations are complex.
- Hides away the real HW structure behind dynamic indexing: at the end of the day, HW vector sizes are generally fixed and multiple vectors will be needed to hold a vector that is larger than the HW.
- Unlikely peephole optimizations will result in good code: arbitrary dynamic accesses, especially at HW vector boundaries unlikely to result in regular patterns.
Discussion ¶
HW Vectors and Implications on the SW and the Programming Model ¶
As of today, the LLVM model only support 1-D vector types. This is
unsurprising because historically, the vast majority of HW only supports 1-D
vector registers. We note that multiple HW vendors are in the process of
evolving to higher-dimensional physical vectors.
In the following discussion, let’s assume the HW vector size is 1-D and the SW
vector size is n-D, with n >= 1. The same discussion would apply with 2-D
HW vector size and n >= 2. In this context, most HW exhibit a vector
register file. The number of such vectors is fixed. Depending on the rank and
sizes of the SW vector abstraction and the HW vector sizes and number of
registers, an n-D SW vector type may be materialized by a mix of multiple
1-D HW vector registers + memory locations at a given point in time.
The implication of the physical HW constraints on the programming model are that
one cannot index dynamically across hardware registers: a register file can
generally not be indexed dynamically. This is because the register number is
fixed and one either needs to unroll explicitly to obtain fixed register numbers
or go through memory. This is a constraint familiar to CUDA programmers: when
declaring a private float a[4]; and subsequently indexing with a dynamic
value results in so-called local memory usage (i.e. roundtripping to
memory).
Implication on codegen ¶
MLIR n-D vector types are currently represented as (n-1)-D arrays of 1-D
vectors when lowered to LLVM. This introduces the consequences on static vs
dynamic indexing discussed previously: extractelement, insertelement and
shufflevector on n-D vectors in MLIR only support static indices. Dynamic
indices are only supported on the most minor 1-D vector but not the outer
(n-1)-D. For other cases, explicit load / stores are required.
The implications on codegen are as follows:
- Loops around
vectorvalues are indirect addressing of vector values, they must operate on explicit load / store operations overn-Dvector types. - Once an
n-Dvectortype is loaded into an SSA value (that may or may not live innregisters, with or without spilling, when eventually lowered), it may be unrolled to smallerk-Dvectortypes and operations that correspond to the HW. This level of MLIR codegen is related to register allocation and spilling that occur much later in the LLVM pipeline. - HW may support >1-D vectors with intrinsics for indirect addressing within
these vectors. These can be targeted thanks to explicit
vector_castoperations from MLIRk-Dvector types and operations to LLVM1-Dvectors + intrinsics.
Alternatively, we argue that directly lowering to a linearized abstraction hides away the codegen complexities related to memory accesses by giving a false impression of magical dynamic indexing across registers. Instead we prefer to make those very explicit in MLIR and allow codegen to explore tradeoffs. Different HW will require different tradeoffs in the sizes involved in steps 1., 2. and 3.
Decisions made at the MLIR level will have implications at a much later stage in
LLVM (after register allocation). We do not envision to expose concerns related
to modeling of register allocation and spilling to MLIR explicitly. Instead,
each target will expose a set of “good” target operations and n-D vector
types, associated with costs that PatterRewriters at the MLIR level will be
able to target. Such costs at the MLIR level will be abstract and used for
ranking, not for accurate performance modeling. In the future such costs will be
learned.
Implication on Lowering to Accelerators ¶
To target accelerators that support higher dimensional vectors natively, we can
start from either 1-D or n-D vectors in MLIR and use vector.cast to
flatten the most minor dimensions to 1-D vector<Kxf32> where K is an
appropriate constant. Then, the existing lowering to LLVM-IR immediately
applies, with extensions for accelerator-specific intrinsics.
It is the role of an Accelerator-specific vector dialect (see codegen flow in
the figure above) to lower the vector.cast. Accelerator -> LLVM lowering would
then consist of a bunch of Accelerator -> Accelerator rewrites to perform the
casts composed with Accelerator -> LLVM conversions + intrinsics that operate
on 1-D vector<Kxf32>.
Some of those rewrites may need extra handling, especially if a reduction is
involved. For example, vector.cast %0: vector<K1x...xKnxf32> to vector<Kxf32>
when K != K1 * … * Kn and some arbitrary irregular vector.cast %0: vector<4x4x17xf32> to vector<Kxf32> may introduce masking and intra-vector
shuffling that may not be worthwhile or even feasible, i.e. infinite cost.
However vector.cast %0: vector<K1x...xKnxf32> to vector<Kxf32> when K = K1 * … * Kn should be close to a noop.
As we start building accelerator-specific abstractions, we hope to achieve retargetable codegen: the same infra is used for CPU, GPU and accelerators with extra MLIR patterns and costs.
Implication on calling external functions that operate on vectors ¶
It is possible (likely) that we additionally need to linearize when calling an external function.
Relationship to LLVM matrix type proposal. ¶
The LLVM matrix proposal was formulated 1 year ago but seemed to be somewhat stalled until recently. In its current form, it is limited to 2-D matrix types and operations are implemented with LLVM intrinsics. In contrast, MLIR sits at a higher level of abstraction and allows the lowering of generic operations on generic n-D vector types from MLIR to aggregates of 1-D LLVM vectors. In the future, it could make sense to lower to the LLVM matrix abstraction also for CPU even though MLIR will continue needing higher level abstractions.
On the other hand, one should note that as MLIR is moving to LLVM, this document could become the unifying abstraction that people should target for 1-D vectors and the LLVM matrix proposal can be viewed as a subset of this work.
Conclusion ¶
The flattened 1-D vector design in the LLVM matrix proposal is good in a HW-specific world with special intrinsics. This is a good abstraction for register allocation, Instruction-Level-Parallelism and SoftWare-Pipelining/Modulo Scheduling optimizations at the register level. However MLIR codegen operates at a higher level of abstraction where we want to target operations on coarser-grained vectors than the HW size and on which unroll-and-jam is applied and patterns across multiple HW vectors can be matched.
This makes “nested aggregate type of 1-D vector” an appealing abstraction for lowering from MLIR because:
- it does not hide complexity related to the buffer vs value semantics and the memory subsystem and
- it does not rely on LLVM to magically make all the things work from a too low-level abstraction.
The use of special intrinsics in a 1-D LLVM world is still available thanks to
an explicit vector.cast op.
Operations ¶
vector.vscale (vector::VectorScaleOp) ¶
Load vector scale size
Syntax:
operation ::= `vector.vscale` attr-dict
The vscale op returns the scale of the scalable vectors, a positive
integer value that is constant at runtime but unknown at compile-time.
The scale of the vector indicates the multiplicity of the vectors and
vector operations. For example, a vector<[4]xi32> is equivalent to
vscale consecutive vector<4xi32>; and an operation on a
vector<[4]xi32> is equivalent to performing that operation vscale
times, once on each <4xi32> segment of the scalable vector. The vscale
op can be used to calculate the step in vector-length agnostic (VLA) loops.
Right now we only support one contiguous set of scalable dimensions, all of
them grouped and scaled with the value returned by ‘vscale’.
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface), OpAsmOpInterface
Effects: MemoryEffects::Effect{}
Results: ¶
| Result | Description |
|---|---|
res | index |
vector.bitcast (vector::BitCastOp) ¶
Bitcast casts between vectors
Syntax:
operation ::= `vector.bitcast` $source attr-dict `:` type($source) `to` type($result)
The bitcast operation casts between vectors of the same rank, the minor 1-D vector size is casted to a vector with a different element type but same bitwidth. In case of 0-D vectors, the bitwidth of element types must be equal.
Example:
// Example casting to a smaller element type.
%1 = vector.bitcast %0 : vector<5x1x4x3xf32> to vector<5x1x4x6xi16>
// Example casting to a bigger element type.
%3 = vector.bitcast %2 : vector<10x12x8xi8> to vector<10x12x2xi32>
// Example casting to an element type of the same size.
%5 = vector.bitcast %4 : vector<5x1x4x3xf32> to vector<5x1x4x3xi32>
// Example casting of 0-D vectors.
%7 = vector.bitcast %6 : vector<f32> to vector<i32>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Operands: ¶
| Operand | Description |
|---|---|
source | vector of any type values |
Results: ¶
| Result | Description |
|---|---|
result | vector of any type values |
vector.broadcast (vector::BroadcastOp) ¶
Broadcast operation
Syntax:
operation ::= `vector.broadcast` $source attr-dict `:` type($source) `to` type($vector)
Broadcasts the scalar or k-D vector value in the source operand to a n-D result vector such that the broadcast makes sense, i.e., the source operand is duplicated to match the given rank and sizes in the result vector. The legality rules are:
- the source operand must have the same element type as the result type
- a k-D vector <s_1 x .. x s_k x type> can be broadcast to
a n-D vector <t_1 x .. x t_n x type> if
- k <= n, and
- the sizes in the trailing dimensions n-k < i <= n with j=i+k-n match exactly as s_j = t_i or s_j = 1:
t_1 x .. t_n-k x t_n-k+1 x .. x t_i x .. x t_n s_1 x .. x s_j x .. x s_k <duplication> <potential stretch>
The source operand is duplicated over all the missing leading dimensions and stretched over the trailing dimensions where the source has a non-equal dimension of 1. These rules imply that any scalar broadcast (k=0) to any shaped vector with the same element type is always legal.
Example:
%0 = arith.constant 0.0 : f32
%1 = vector.broadcast %0 : f32 to vector<16xf32>
%2 = vector.broadcast %1 : vector<16xf32> to vector<4x16xf32>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Operands: ¶
| Operand | Description |
|---|---|
source | any type |
Results: ¶
| Result | Description |
|---|---|
vector | vector of any type values |
vector.compressstore (vector::CompressStoreOp) ¶
Writes elements selectively from a vector as defined by a mask
Syntax:
operation ::= `vector.compressstore` $base `[` $indices `]` `,` $mask `,` $valueToStore attr-dict `:` type($base) `,` type($mask) `,` type($valueToStore)
The compress store operation writes elements from a 1-D vector into memory as defined by a base with indices and a 1-D mask vector. When the mask is set, the corresponding element from the vector is written next to memory. Otherwise, no action is taken for the element. Informally the semantics are:
index = i
if (mask[0]) base[index++] = value[0]
if (mask[1]) base[index++] = value[1]
etc.
Note that the index increment is done conditionally.
If a mask bit is set and the corresponding index is out-of-bounds for the given base, the behavior is undefined. If a mask bit is not set, no value is stored regardless of the index, and the index is allowed to be out-of-bounds.
The compress store can be used directly where applicable, or can be used
during progressively lowering to bring other memory operations closer to
hardware ISA support for a compress. The semantics of the operation closely
correspond to those of the llvm.masked.compressstore
intrinsic.
Examples:
vector.compressstore %base[%i], %mask, %value
: memref<?xf32>, vector<8xi1>, vector<8xf32>
vector.compressstore %base[%i, %j], %mask, %value
: memref<?x?xf32>, vector<16xi1>, vector<16xf32>
Operands: ¶
| Operand | Description |
|---|---|
base | memref of any type values |
indices | variadic of index |
mask | vector of 1-bit signless integer values of ranks 1 |
valueToStore | of ranks 1 |
vector.constant_mask (vector::ConstantMaskOp) ¶
Creates a constant vector mask
Syntax:
operation ::= `vector.constant_mask` $mask_dim_sizes attr-dict `:` type(results)
Creates and returns a vector mask where elements of the result vector are set to ‘0’ or ‘1’, based on whether the element indices are contained within a hyper-rectangular region specified by the ‘mask_dim_sizes’ array attribute argument. Each element of the ‘mask_dim_sizes’ array, specifies an exclusive upper bound [0, mask-dim-size-element-value) for a unique dimension in the vector result. The conjunction of the ranges define a hyper-rectangular region within which elements values are set to 1 (otherwise element values are set to 0). Each value of ‘mask_dim_sizes’ must be non-negative and not greater than the size of the corresponding vector dimension (as opposed to vector.create_mask which allows this). Sizes that correspond to scalable dimensions are implicitly multiplied by vscale, though currently only zero (none set) or the size of the dim/vscale (all set) are supported.
Example:
// create a constant vector mask of size 4x3xi1 with elements in range
// 0 <= row <= 2 and 0 <= col <= 1 are set to 1 (others to 0).
%1 = vector.constant_mask [3, 2] : vector<4x3xi1>
print %1
columns
0 1 2
|------------
0 | 1 1 0
rows 1 | 1 1 0
2 | 1 1 0
3 | 0 0 0
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
mask_dim_sizes | ::mlir::ArrayAttr | 64-bit integer array attribute |
Results: ¶
| Result | Description |
|---|---|
| «unnamed» | vector of 1-bit signless integer values |
vector.contract (vector::ContractionOp) ¶
Vector contraction operation
Computes the sum of products of vector elements along contracting dimension pairs from 2 vectors of rank M and N respectively, adds this intermediate result to the accumulator argument of rank K, and returns a vector result of rank K (where K = num_lhs_free_dims + num_rhs_free_dims + num_batch_dims (see dimension type descriptions below)). For K = 0 (no free or batch dimensions), the accumulator and output are a scalar.
If operands and the result have types of different bitwidths, operands are promoted to have the same bitwidth as the result before performing the contraction. For integer types, only signless integer types are supported, and the promotion happens via sign extension.
An iterator type attribute list must be specified, where each element of the list represents an iterator with one of the following types:
“reduction”: reduction dimensions are present in the lhs and rhs arguments but not in the output (and accumulator argument). These are the dimensions along which the vector contraction op computes the sum of products, and contracting dimension pair dimension sizes must match between lhs/rhs.
“parallel”: Batch dimensions are iterator type “parallel”, and are non-contracting dimensions present in the lhs, rhs and output. The lhs/rhs co-iterate along the batch dimensions, which should be expressed in their indexing maps.
Free dimensions are iterator type “parallel”, and are non-contraction, non-batch dimensions accessed by either the lhs or rhs (but not both). The lhs and rhs free dimensions are unrelated to each other and do not co-iterate, which should be expressed in their indexing maps.
An indexing map attribute list must be specified with an entry for lhs, rhs and acc arguments. An indexing map attribute specifies a mapping from each iterator in the iterator type list, to each dimension of an N-D vector.
An optional kind attribute may be used to specify the combining function
between the intermediate result and accumulator argument of rank K. This
attribute can take the values add/mul/minsi/minui/maxsi/maxui
/and/or/xor for integers, and add/mul/minnumf/maxnumf
/minimumf/maximumf for floats. The default is add.
Example:
// Simple DOT product (K = 0).
#contraction_accesses = [
affine_map<(i) -> (i)>,
affine_map<(i) -> (i)>,
affine_map<(i) -> ()>
]
#contraction_trait = {
indexing_maps = #contraction_accesses,
iterator_types = ["reduction"]
}
%3 = vector.contract #contraction_trait %0, %1, %2
: vector<10xf32>, vector<10xf32> into f32
// 2D vector contraction with one contracting dimension (matmul, K = 2).
#contraction_accesses = [
affine_map<(i, j, k) -> (i, k)>,
affine_map<(i, j, k) -> (k, j)>,
affine_map<(i, j, k) -> (i, j)>
]
#contraction_trait = {
indexing_maps = #contraction_accesses,
iterator_types = ["parallel", "parallel", "reduction"]
}
%3 = vector.contract #contraction_trait %0, %1, %2
: vector<4x3xf32>, vector<3x7xf32> into vector<4x7xf32>
// 4D to 3D vector contraction with two contracting dimensions and
// one batch dimension (K = 3).
#contraction_accesses = [
affine_map<(b0, f0, f1, c0, c1) -> (c0, b0, c1, f0)>,
affine_map<(b0, f0, f1, c0, c1) -> (b0, c1, c0, f1)>,
affine_map<(b0, f0, f1, c0, c1) -> (b0, f0, f1)>
]
#contraction_trait = {
indexing_maps = #contraction_accesses,
iterator_types = ["parallel", "parallel", "parallel",
"reduction", "reduction"]
}
%4 = vector.contract #contraction_trait %0, %1, %2
: vector<7x8x16x15xf32>, vector<8x16x7x5xf32> into vector<8x15x5xf32>
// Vector contraction with mixed typed. lhs/rhs have different element
// types than accumulator/result.
%5 = vector.contract #contraction_trait %0, %1, %2
: vector<10xf16>, vector<10xf16> into f32
// Contract with max (K = 0).
#contraction_accesses = [
affine_map<(i) -> (i)>,
affine_map<(i) -> (i)>,
affine_map<(i) -> ()>
]
#contraction_trait = {
indexing_maps = #contraction_accesses,
iterator_types = ["reduction"],
kind = #vector.kind<maxnumf>
}
%6 = vector.contract #contraction_trait %0, %1, %2
: vector<10xf32>, vector<10xf32> into f32
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, MaskableOpInterface, NoMemoryEffect (MemoryEffectOpInterface), VectorUnrollOpInterface
Effects: MemoryEffects::Effect{}
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
indexing_maps | ::mlir::ArrayAttr | array attribute |
iterator_types | ::mlir::ArrayAttr | Iterator type should be an enum. |
kind | ::mlir::vector::CombiningKindAttr | Kind of combining function for contractions and reductionsEnum cases:
|
Operands: ¶
| Operand | Description |
|---|---|
lhs | vector of any type values |
rhs | vector of any type values |
acc | any type |
Results: ¶
| Result | Description |
|---|---|
| «unnamed» | any type |
vector.create_mask (vector::CreateMaskOp) ¶
Creates a vector mask
Syntax:
operation ::= `vector.create_mask` $operands attr-dict `:` type(results)
Creates and returns a vector mask where elements of the result vector are set to ‘0’ or ‘1’, based on whether the element indices are contained within a hyper-rectangular region specified by the operands. Specifically, each operand specifies a range [0, operand-value) for a unique dimension in the vector result. The conjunction of the operand ranges define a hyper-rectangular region within which elements values are set to 1 (otherwise element values are set to 0). If operand-value is negative, it is treated as if it were zero, and if it is greater than the corresponding dimension size, it is treated as if it were equal to the dimension size.
Example:
// create a vector mask of size 4x3xi1 where elements in range
// 0 <= row <= 2 and 0 <= col <= 1 are set to 1 (others to 0).
%1 = vector.create_mask %c3, %c2 : vector<4x3xi1>
print %1
columns
0 1 2
|------------
0 | 1 1 0
rows 1 | 1 1 0
2 | 1 1 0
3 | 0 0 0
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Operands: ¶
| Operand | Description |
|---|---|
operands | variadic of index |
Results: ¶
| Result | Description |
|---|---|
| «unnamed» | vector of 1-bit signless integer values |
vector.deinterleave (vector::DeinterleaveOp) ¶
Constructs two vectors by deinterleaving an input vector
Syntax:
operation ::= `vector.deinterleave` $source attr-dict `:` type($source) `->` type($res1)
The deinterleave operation constructs two vectors from a single input
vector. The first result vector contains the elements from even indexes
of the input, and the second contains elements from odd indexes. This is
the inverse of a vector.interleave operation.
Each output’s trailing dimension is half of the size of the input vector’s trailing dimension. This operation requires the input vector to have a rank > 0 and an even number of elements in its trailing dimension.
The operation supports scalable vectors.
Example:
%0, %1 = vector.deinterleave %a
: vector<8xi8> -> vector<4xi8>
%2, %3 = vector.deinterleave %b
: vector<2x8xi8> -> vector<2x4xi8>
%4, %5 = vector.deinterleave %c
: vector<2x8x4xi8> -> vector<2x8x2xi8>
%6, %7 = vector.deinterleave %d
: vector<[8]xf32> -> vector<[4]xf32>
%8, %9 = vector.deinterleave %e
: vector<2x[6]xf64> -> vector<2x[3]xf64>
%10, %11 = vector.deinterleave %f
: vector<2x4x[6]xf64> -> vector<2x4x[3]xf64>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Operands: ¶
| Operand | Description |
|---|---|
source | vector of any type values |
Results: ¶
| Result | Description |
|---|---|
res1 | vector of any type values |
res2 | vector of any type values |
vector.expandload (vector::ExpandLoadOp) ¶
Reads elements from memory and spreads them into a vector as defined by a mask
Syntax:
operation ::= `vector.expandload` $base `[` $indices `]` `,` $mask `,` $pass_thru attr-dict `:` type($base) `,` type($mask) `,` type($pass_thru) `into` type($result)
The expand load reads elements from memory into a 1-D vector as defined by a base with indices and a 1-D mask vector. When the mask is set, the next element is read from memory. Otherwise, the corresponding element is taken from a 1-D pass-through vector. Informally the semantics are:
index = i
result[0] := if mask[0] then base[index++] else pass_thru[0]
result[1] := if mask[1] then base[index++] else pass_thru[1]
etc.
Note that the index increment is done conditionally.
If a mask bit is set and the corresponding index is out-of-bounds for the given base, the behavior is undefined. If a mask bit is not set, the value comes from the pass-through vector regardless of the index, and the index is allowed to be out-of-bounds.
The expand load can be used directly where applicable, or can be used
during progressively lowering to bring other memory operations closer to
hardware ISA support for an expand. The semantics of the operation closely
correspond to those of the llvm.masked.expandload
intrinsic.
Examples:
%0 = vector.expandload %base[%i], %mask, %pass_thru
: memref<?xf32>, vector<8xi1>, vector<8xf32> into vector<8xf32>
%1 = vector.expandload %base[%i, %j], %mask, %pass_thru
: memref<?x?xf32>, vector<16xi1>, vector<16xf32> into vector<16xf32>
Operands: ¶
| Operand | Description |
|---|---|
base | memref of any type values |
indices | variadic of index |
mask | vector of 1-bit signless integer values of ranks 1 |
pass_thru | of ranks 1 |
Results: ¶
| Result | Description |
|---|---|
result | of ranks 1 |
vector.extractelement (vector::ExtractElementOp) ¶
Extractelement operation
Syntax:
operation ::= `vector.extractelement` $vector `[` ($position^ `:` type($position))? `]` attr-dict `:` type($vector)
Takes a 0-D or 1-D vector and a optional dynamic index position and extracts the scalar at that position.
Note that this instruction resembles vector.extract, but is restricted to 0-D and 1-D vectors and relaxed to dynamic indices. If the vector is 0-D, the position must be std::nullopt.
It is meant to be closer to LLVM’s version: https://llvm.org/docs/LangRef.html#extractelement-instruction
Example:
%c = arith.constant 15 : i32
%1 = vector.extractelement %0[%c : i32]: vector<16xf32>
%2 = vector.extractelement %z[]: vector<f32>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Operands: ¶
| Operand | Description |
|---|---|
vector | vector of any type values |
position | signless integer or index |
Results: ¶
| Result | Description |
|---|---|
result | any type |
vector.extract (vector::ExtractOp) ¶
Extract operation
Syntax:
operation ::= `vector.extract` $vector ``
custom<DynamicIndexList>($dynamic_position, $static_position)
attr-dict `:` type($result) `from` type($vector)
Takes an n-D vector and a k-D position and extracts the (n-k)-D vector at the proper position. Degenerates to an element type if n-k is zero.
Dynamic indices must be greater or equal to zero and less than the size of the corresponding dimension. The result is undefined if any index is out-of-bounds.
Example:
%1 = vector.extract %0[3]: vector<8x16xf32> from vector<4x8x16xf32>
%2 = vector.extract %0[2, 1, 3]: f32 from vector<4x8x16xf32>
%3 = vector.extract %1[]: vector<f32> from vector<f32>
%4 = vector.extract %0[%a, %b, %c]: f32 from vector<4x8x16xf32>
%5 = vector.extract %0[2, %b]: vector<16xf32> from vector<4x8x16xf32>
Traits: AlwaysSpeculatableImplTrait, InferTypeOpAdaptor
Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
static_position | ::mlir::DenseI64ArrayAttr | i64 dense array attribute |
Operands: ¶
| Operand | Description |
|---|---|
vector | vector of any type values |
dynamic_position | variadic of index |
Results: ¶
| Result | Description |
|---|---|
result | any type |
vector.extract_strided_slice (vector::ExtractStridedSliceOp) ¶
Extract_strided_slice operation
Syntax:
operation ::= `vector.extract_strided_slice` $vector attr-dict `:` type($vector) `to` type(results)
Takes an n-D vector, k-D offsets integer array attribute, a k-sized
sizes integer array attribute, a k-sized strides integer array
attribute and extracts the n-D subvector at the proper offset.
At the moment strides must contain only 1s.
Returns an n-D vector where the first k-D dimensions match the sizes
attribute. The returned subvector contains the elements starting at offset
offsets and ending at offsets + sizes.
Example:
%1 = vector.extract_strided_slice %0
{offsets = [0, 2], sizes = [2, 4], strides = [1, 1]}:
vector<4x8x16xf32> to vector<2x4x16xf32>
// TODO: Evolve to a range form syntax similar to:
%1 = vector.extract_strided_slice %0[0:2:1][2:4:1]
vector<4x8x16xf32> to vector<2x4x16xf32>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
offsets | ::mlir::ArrayAttr | 64-bit integer array attribute |
sizes | ::mlir::ArrayAttr | 64-bit integer array attribute |
strides | ::mlir::ArrayAttr | 64-bit integer array attribute |
Operands: ¶
| Operand | Description |
|---|---|
vector | vector of any type values |
Results: ¶
| Result | Description |
|---|---|
| «unnamed» | vector of any type values |
vector.fma (vector::FMAOp) ¶
Vector fused multiply-add
Syntax:
operation ::= `vector.fma` $lhs `,` $rhs `,` $acc attr-dict `:` type($lhs)
Multiply-add expressions operate on n-D vectors and compute a fused
pointwise multiply-and-accumulate: $result = $lhs * $rhs + $acc. All operands and result have the same vector type. The semantics of the operation correspond to those of the llvm.fma[intrinsic](https://llvm.org/docs/LangRef.html#int-fma). In the particular case of lowering to LLVM, this is guaranteed to lower to thellvm.fma.*` intrinsic.
Example:
%3 = vector.fma %0, %1, %2: vector<8x16xf32>
Traits: AlwaysSpeculatableImplTrait, Elementwise, Scalarizable, Tensorizable, Vectorizable
Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface), VectorUnrollOpInterface
Effects: MemoryEffects::Effect{}
Operands: ¶
| Operand | Description |
|---|---|
lhs | vector of floating-point values |
rhs | vector of floating-point values |
acc | vector of floating-point values |
Results: ¶
| Result | Description |
|---|---|
result | vector of floating-point values |
vector.flat_transpose (vector::FlatTransposeOp) ¶
Vector matrix transposition on flattened 1-D MLIR vectors
Syntax:
operation ::= `vector.flat_transpose` $matrix attr-dict `:` type($matrix) `->` type($res)
This is the counterpart of llvm.matrix.transpose in MLIR. It serves the purposes of more progressive lowering and localized type conversion. Higher levels typically lower matrix tranpositions into ‘vector.transpose’ operations. Subsequent rewriting rule progressively lower these operations into ‘vector.flat_transpose’ operations to bring the operations closer to the hardware ISA.
The vector.flat_transpose op treats the 1-D input matrix as
a 2-D matrix with
Also see:
http://llvm.org/docs/LangRef.html#llvm-matrix-transpose-intrinsic
Example:
%1 = vector.flat_transpose %0 {columns = 4 : i32, rows = 4 : i32}
: vector<16xf32> -> vector<16xf32>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
rows | ::mlir::IntegerAttr | 32-bit signless integer attribute |
columns | ::mlir::IntegerAttr | 32-bit signless integer attribute |
Operands: ¶
| Operand | Description |
|---|---|
matrix | vector of signless integer or signed integer or index or floating-point values of ranks 1 |
Results: ¶
| Result | Description |
|---|---|
res | vector of signless integer or signed integer or index or floating-point values of ranks 1 |
vector.from_elements (vector::FromElementsOp) ¶
Operation that defines a vector from scalar elements
Syntax:
operation ::= `vector.from_elements` $elements attr-dict `:` type($result)
This operation defines a vector from one or multiple scalar elements. The number of elements must match the number of elements in the result type. All elements must have the same type, which must match the element type of the result vector type.
elements are a flattened version of the result vector in row-major order.
Example:
// %f1
%0 = vector.from_elements %f1 : vector<f32>
// [%f1, %f2]
%1 = vector.from_elements %f1, %f2 : vector<2xf32>
// [[%f1, %f2, %f3], [%f4, %f5, %f6]]
%2 = vector.from_elements %f1, %f2, %f3, %f4, %f5, %f6 : vector<2x3xf32>
// [[[%f1, %f2]], [[%f3, %f4]], [[%f5, %f6]]]
%3 = vector.from_elements %f1, %f2, %f3, %f4, %f5, %f6 : vector<3x1x2xf32>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Operands: ¶
| Operand | Description |
|---|---|
elements | variadic of any type |
Results: ¶
| Result | Description |
|---|---|
result | vector of any type values |
vector.gather (vector::GatherOp) ¶
Gathers elements from memory or ranked tensor into a vector as defined by an index vector and a mask vector
Syntax:
operation ::= `vector.gather` $base `[` $indices `]` `[` $index_vec `]` `,` $mask `,` $pass_thru attr-dict `:` type($base) `,` type($index_vec) `,` type($mask) `,` type($pass_thru) `into` type($result)
The gather operation returns an n-D vector whose elements are either loaded from memory or ranked tensor, or taken from a pass-through vector, depending on the values of an n-D mask vector. If a mask bit is set, the corresponding result element is defined by the base with indices and the n-D index vector (each index is a 1-D offset on the base). Otherwise, the corresponding element is taken from the n-D pass-through vector. Informally the semantics are:
result[0] := if mask[0] then base[index[0]] else pass_thru[0]
result[1] := if mask[1] then base[index[1]] else pass_thru[1]
etc.
If a mask bit is set and the corresponding index is out-of-bounds for the given base, the behavior is undefined. If a mask bit is not set, the value comes from the pass-through vector regardless of the index, and the index is allowed to be out-of-bounds.
The gather operation can be used directly where applicable, or can be used during progressively lowering to bring other memory operations closer to hardware ISA support for a gather.
Examples:
%0 = vector.gather %base[%c0][%v], %mask, %pass_thru
: memref<?xf32>, vector<2x16xi32>, vector<2x16xi1>, vector<2x16xf32> into vector<2x16xf32>
%1 = vector.gather %base[%i, %j][%v], %mask, %pass_thru
: memref<16x16xf32>, vector<16xi32>, vector<16xi1>, vector<16xf32> into vector<16xf32>
Interfaces: MaskableOpInterface, VectorUnrollOpInterface
Operands: ¶
| Operand | Description |
|---|---|
base | shaped of any type values |
indices | variadic of index |
index_vec | vector of integer or index values |
mask | vector of 1-bit signless integer values |
pass_thru | vector of any type values |
Results: ¶
| Result | Description |
|---|---|
result | vector of any type values |
vector.insertelement (vector::InsertElementOp) ¶
Insertelement operation
Syntax:
operation ::= `vector.insertelement` $source `,` $dest `[` ($position^ `:` type($position))? `]` attr-dict `:`
type($result)
Takes a scalar source, a 0-D or 1-D destination vector and a dynamic index position and inserts the source into the destination at the proper position.
Note that this instruction resembles vector.insert, but is restricted to 0-D and 1-D vectors and relaxed to dynamic indices.
It is meant to be closer to LLVM’s version: https://llvm.org/docs/LangRef.html#insertelement-instruction
Example:
%c = arith.constant 15 : i32
%f = arith.constant 0.0f : f32
%1 = vector.insertelement %f, %0[%c : i32]: vector<16xf32>
%2 = vector.insertelement %f, %z[]: vector<f32>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Operands: ¶
| Operand | Description |
|---|---|
source | any type |
dest | vector of any type values |
position | signless integer or index |
Results: ¶
| Result | Description |
|---|---|
result | vector of any type values |
vector.insert (vector::InsertOp) ¶
Insert operation
Syntax:
operation ::= `vector.insert` $source `,` $dest custom<DynamicIndexList>($dynamic_position, $static_position)
attr-dict `:` type($source) `into` type($dest)
Takes an n-D source vector, an (n+k)-D destination vector and a k-D position and inserts the n-D source into the (n+k)-D destination at the proper position. Degenerates to a scalar or a 0-d vector source type when n = 0.
Dynamic indices must be greater or equal to zero and less than the size of the corresponding dimension. The result is undefined if any index is out-of-bounds.
Example:
%2 = vector.insert %0, %1[3] : vector<8x16xf32> into vector<4x8x16xf32>
%5 = vector.insert %3, %4[2, 1, 3] : f32 into vector<4x8x16xf32>
%8 = vector.insert %6, %7[] : f32 into vector<f32>
%11 = vector.insert %9, %10[%a, %b, %c] : vector<f32> into vector<4x8x16xf32>
%12 = vector.insert %4, %10[2, %b] : vector<16xf32> into vector<4x8x16xf32>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
static_position | ::mlir::DenseI64ArrayAttr | i64 dense array attribute |
Operands: ¶
| Operand | Description |
|---|---|
source | any type |
dest | vector of any type values |
dynamic_position | variadic of index |
Results: ¶
| Result | Description |
|---|---|
result | vector of any type values |
vector.insert_strided_slice (vector::InsertStridedSliceOp) ¶
Strided_slice operation
Syntax:
operation ::= `vector.insert_strided_slice` $source `,` $dest attr-dict `:` type($source) `into` type($dest)
Takes a k-D source vector, an n-D destination vector (n >= k), n-sized
offsets integer array attribute, a k-sized strides integer array attribute
and inserts the k-D source vector as a strided subvector at the proper offset
into the n-D destination vector.
At the moment strides must contain only 1s.
Returns an n-D vector that is a copy of the n-D destination vector in which the last k-D dimensions contain the k-D source vector elements strided at the proper location as specified by the offsets.
Example:
%2 = vector.insert_strided_slice %0, %1
{offsets = [0, 0, 2], strides = [1, 1]}:
vector<2x4xf32> into vector<16x4x8xf32>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
offsets | ::mlir::ArrayAttr | 64-bit integer array attribute |
strides | ::mlir::ArrayAttr | 64-bit integer array attribute |
Operands: ¶
| Operand | Description |
|---|---|
source | vector of any type values |
dest | vector of any type values |
Results: ¶
| Result | Description |
|---|---|
res | vector of any type values |
vector.interleave (vector::InterleaveOp) ¶
Constructs a vector by interleaving two input vectors
Syntax:
operation ::= `vector.interleave` $lhs `,` $rhs attr-dict `:` type($lhs) `->` type($result)
The interleave operation constructs a new vector by interleaving the elements from the trailing (or final) dimension of two input vectors, returning a new vector where the trailing dimension is twice the size.
Note that for the n-D case this differs from the interleaving possible with
vector.shuffle, which would only operate on the leading dimension.
Another key difference is this operation supports scalable vectors, though currently a general LLVM lowering is limited to the case where only the trailing dimension is scalable.
Example:
%a = arith.constant dense<[0, 1]> : vector<2xi32>
%b = arith.constant dense<[2, 3]> : vector<2xi32>
// The value of `%0` is `[0, 2, 1, 3]`.
%0 = vector.interleave %a, %b : vector<2xi32> -> vector<4xi32>
// Examples showing allowed input and result types.
%1 = vector.interleave %c, %d : vector<f16> -> vector<2xf16>
%2 = vector.interleave %e, %f : vector<6x3xf32> -> vector<6x6xf32>
%3 = vector.interleave %g, %h : vector<[4]xi32> -> vector<[8]xi32>
%4 = vector.interleave %i, %j : vector<2x4x[2]xf64> -> vector<2x4x[4]xf64>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Operands: ¶
| Operand | Description |
|---|---|
lhs | vector of any type values |
rhs | vector of any type values |
Results: ¶
| Result | Description |
|---|---|
result | vector of any type values |
vector.load (vector::LoadOp) ¶
Reads an n-D slice of memory into an n-D vector
Syntax:
operation ::= `vector.load` $base `[` $indices `]` attr-dict `:` type($base) `,` type($result)
The ‘vector.load’ operation reads an n-D slice of memory into an n-D vector. It takes a ‘base’ memref, an index for each memref dimension and a result vector type as arguments. It returns a value of the result vector type. The ‘base’ memref and indices determine the start memory address from which to read. Each index provides an offset for each memref dimension based on the element type of the memref. The shape of the result vector type determines the shape of the slice read from the start memory address. The elements along each dimension of the slice are strided by the memref strides. Only unit strides are allowed along the most minor memref dimension. These constraints guarantee that elements read along the first dimension of the slice are contiguous in memory.
The memref element type can be a scalar or a vector type. If the memref element type is a scalar, it should match the element type of the result vector. If the memref element type is vector, it should match the result vector type.
Example: 0-D vector load on a scalar memref.
%result = vector.load %base[%i, %j] : memref<100x100xf32>, vector<f32>
Example: 1-D vector load on a scalar memref.
%result = vector.load %base[%i, %j] : memref<100x100xf32>, vector<8xf32>
Example: 1-D vector load on a vector memref.
%result = vector.load %memref[%i, %j] : memref<200x100xvector<8xf32>>, vector<8xf32>
Example: 2-D vector load on a scalar memref.
%result = vector.load %memref[%i, %j] : memref<200x100xf32>, vector<4x8xf32>
Example: 2-D vector load on a vector memref.
%result = vector.load %memref[%i, %j] : memref<200x100xvector<4x8xf32>>, vector<4x8xf32>
Representation-wise, the ‘vector.load’ operation permits out-of-bounds reads. Support and implementation of out-of-bounds vector loads is target-specific. No assumptions should be made on the value of elements loaded out of bounds. Not all targets may support out-of-bounds vector loads.
Example: Potential out-of-bound vector load.
%result = vector.load %memref[%index] : memref<?xf32>, vector<8xf32>
Example: Explicit out-of-bound vector load.
%result = vector.load %memref[%c0] : memref<7xf32>, vector<8xf32>
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
nontemporal | ::mlir::BoolAttr | bool attribute |
Operands: ¶
| Operand | Description |
|---|---|
base | memref of any type values |
indices | variadic of index |
Results: ¶
| Result | Description |
|---|---|
result | vector of any type values |
vector.mask (vector::MaskOp) ¶
Predicates a maskable vector operation
The vector.mask is a MaskingOpInterface operation that predicates the
execution of another operation. It takes an i1 vector mask and an
optional passthru vector as arguments.
A implicitly vector.yield-terminated region encloses the operation to be
masked. Values used within the region are captured from above. Only one
maskable operation can be masked with a vector.mask operation at a time.
An operation is maskable if it implements the MaskableOpInterface. The
terminator yields all results of the maskable operation to the result of
this operation.
The vector mask argument holds a bit for each vector lane and determines
which vector lanes should execute the maskable operation and which ones
should not. The vector.mask operation returns the value produced by the
masked execution of the nested operation, if any. The masked-off lanes in
the result vector are taken from the corresponding lanes of the pass-thru
argument, if provided, or left unmodified, otherwise.
The vector.mask operation does not prescribe how a maskable operation
should be masked or how a masked operation should be lowered. Masking
constraints and some semantic details are provided by each maskable
operation through the MaskableOpInterface. Lowering of masked operations
is implementation defined. For instance, scalarizing the masked operation
or executing the operation for the masked-off lanes are valid lowerings as
long as the execution of masked-off lanes does not change the observable
behavior of the program.
Examples:
%0 = vector.mask %mask { vector.reduction <add>, %a : vector<8xi32> into i32 } : vector<8xi1> -> i32
%0 = vector.mask %mask, %passthru { arith.divsi %a, %b : vector<8xi32> } : vector<8xi1> -> vector<8xi32>
vector.mask %mask { vector.transfer_write %val, %t0[%idx] : vector<16xf32>, memref<?xf32> } : vector<16xi1>
vector.mask %mask { vector.transfer_write %val, %t0[%idx] : vector<16xf32>, tensor<?xf32> } : vector<16xi1> -> tensor<?xf32>
Traits: NoRegionArguments, RecursiveMemoryEffects, SingleBlockImplicitTerminator<vector::YieldOp>, SingleBlock
Interfaces: MaskingOpInterface
Operands: ¶
| Operand | Description |
|---|---|
mask | vector of 1-bit signless integer values |
passthru | any type |
Results: ¶
| Result | Description |
|---|---|
results | variadic of any type |
vector.maskedload (vector::MaskedLoadOp) ¶
Loads elements from memory into a vector as defined by a mask vector
Syntax:
operation ::= `vector.maskedload` $base `[` $indices `]` `,` $mask `,` $pass_thru attr-dict `:` type($base) `,` type($mask) `,` type($pass_thru) `into` type($result)
The masked load reads elements from memory into a 1-D vector as defined by a base with indices and a 1-D mask vector. When the mask is set, the element is read from memory. Otherwise, the corresponding element is taken from a 1-D pass-through vector. Informally the semantics are:
result[0] := if mask[0] then base[i + 0] else pass_thru[0]
result[1] := if mask[1] then base[i + 1] else pass_thru[1]
etc.
If a mask bit is set and the corresponding index is out-of-bounds for the given base, the behavior is undefined. If a mask bit is not set, the value comes from the pass-through vector regardless of the index, and the index is allowed to be out-of-bounds.
The masked load can be used directly where applicable, or can be used
during progressively lowering to bring other memory operations closer to
hardware ISA support for a masked load. The semantics of the operation
closely correspond to those of the llvm.masked.load
intrinsic.
Examples:
%0 = vector.maskedload %base[%i], %mask, %pass_thru
: memref<?xf32>, vector<8xi1>, vector<8xf32> into vector<8xf32>
%1 = vector.maskedload %base[%i, %j], %mask, %pass_thru
: memref<?x?xf32>, vector<16xi1>, vector<16xf32> into vector<16xf32>
Operands: ¶
| Operand | Description |
|---|---|
base | memref of any type values |
indices | variadic of index |
mask | vector of 1-bit signless integer values of ranks 1 |
pass_thru | of ranks 1 |
Results: ¶
| Result | Description |
|---|---|
result | of ranks 1 |
vector.maskedstore (vector::MaskedStoreOp) ¶
Stores elements from a vector into memory as defined by a mask vector
Syntax:
operation ::= `vector.maskedstore` $base `[` $indices `]` `,` $mask `,` $valueToStore attr-dict `:` type($base) `,` type($mask) `,` type($valueToStore)
The masked store operation writes elements from a 1-D vector into memory as defined by a base with indices and a 1-D mask vector. When the mask is set, the corresponding element from the vector is written to memory. Otherwise, no action is taken for the element. Informally the semantics are:
if (mask[0]) base[i+0] = value[0]
if (mask[1]) base[i+1] = value[1]
etc.
If a mask bit is set and the corresponding index is out-of-bounds for the given base, the behavior is undefined. If a mask bit is not set, no value is stored regardless of the index, and the index is allowed to be out-of-bounds.
The masked store can be used directly where applicable, or can be used
during progressively lowering to bring other memory operations closer to
hardware ISA support for a masked store. The semantics of the operation
closely correspond to those of the llvm.masked.store
intrinsic.
Examples:
vector.maskedstore %base[%i], %mask, %value
: memref<?xf32>, vector<8xi1>, vector<8xf32>
vector.maskedstore %base[%i, %j], %mask, %value
: memref<?x?xf32>, vector<16xi1>, vector<16xf32>
Operands: ¶
| Operand | Description |
|---|---|
base | memref of any type values |
indices | variadic of index |
mask | vector of 1-bit signless integer values of ranks 1 |
valueToStore | of ranks 1 |
vector.matrix_multiply (vector::MatmulOp) ¶
Vector matrix multiplication op that operates on flattened 1-D MLIR vectors
Syntax:
operation ::= `vector.matrix_multiply` $lhs `,` $rhs attr-dict `:` `(` type($lhs) `,` type($rhs) `)` `->` type($res)
This is the counterpart of llvm.matrix.multiply in MLIR. It serves the purposes of more progressive lowering and localized type conversion. Higher levels typically lower matrix multiplications into ‘vector.contract’ operations. Subsequent rewriting rule progressively lower these operations into ‘vector.matrix_multiply’ operations to bring the operations closer to the hardware ISA.
The ‘vector.matrix_multiply’ op treats lhs as matrix with <lhs_rows> rows
and <lhs_columns> columns, rhs as matrix with <lhs_columns> rows and
<rhs_columns> and multiplies them. The result matrix is returned embedded in
the result vector.
Also see:
http://llvm.org/docs/LangRef.html#llvm-matrix-multiply-intrinsic
Example:
%C = vector.matrix_multiply %A, %B
{ lhs_rows = 4: i32, lhs_columns = 16: i32 , rhs_columns = 3: i32 } :
(vector<64xf64>, vector<48xf64>) -> vector<12xf64>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
lhs_rows | ::mlir::IntegerAttr | 32-bit signless integer attribute |
lhs_columns | ::mlir::IntegerAttr | 32-bit signless integer attribute |
rhs_columns | ::mlir::IntegerAttr | 32-bit signless integer attribute |
Operands: ¶
| Operand | Description |
|---|---|
lhs | vector of signless integer or signed integer or index or floating-point values of ranks 1 |
rhs | vector of signless integer or signed integer or index or floating-point values of ranks 1 |
Results: ¶
| Result | Description |
|---|---|
res | vector of signless integer or signed integer or index or floating-point values of ranks 1 |
vector.multi_reduction (vector::MultiDimReductionOp) ¶
Multi-dimensional reduction operation
Syntax:
operation ::= `vector.multi_reduction` $kind `,` $source `,` $acc attr-dict $reduction_dims `:` type($source) `to` type($dest)
Reduces an n-D vector into an (n-k)-D vector (or a scalar when k == n)
using the given operation: add/mul/minsi/minui/maxsi/maxui
/and/or/xor for integers, and add/mul/minnumf/maxnumf/minimumf
/maximumf for floats.
Takes an initial accumulator operand.
Example:
%1 = vector.multi_reduction <add>, %0, %acc0 [1, 3] :
vector<4x8x16x32xf32> to vector<4x16xf32>
%2 = vector.multi_reduction <add>, %1, %acc1 [0, 1] :
vector<4x16xf32> to f32
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, InferTypeOpInterface, MaskableOpInterface, NoMemoryEffect (MemoryEffectOpInterface), VectorUnrollOpInterface
Effects: MemoryEffects::Effect{}
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
kind | ::mlir::vector::CombiningKindAttr | Kind of combining function for contractions and reductionsEnum cases:
|
reduction_dims | ::mlir::ArrayAttr | 64-bit integer array attribute |
Operands: ¶
| Operand | Description |
|---|---|
source | vector of any type values |
acc | any type |
Results: ¶
| Result | Description |
|---|---|
dest | any type |
vector.outerproduct (vector::OuterProductOp) ¶
Vector outerproduct with optional fused add
Takes 2 1-D vectors and returns the 2-D vector containing the outer-product, as illustrated below:
outer | [c, d]
------+------------
[a, | [ [a*c, a*d],
b] | [b*c, b*d] ]
This operation also accepts a 1-D vector lhs and a scalar rhs. In this case a simple AXPY operation is performed, which returns a 1-D vector.
[a, b] * c = [a*c, b*c]
An optional extra vector argument with the same shape as the output
vector may be specified in which case the operation returns the sum of
the outer-product and the extra vector. In this multiply-accumulate
scenario for floating-point arguments, the rounding mode is enforced
by guaranteeing that a fused-multiply add operation is emitted. When
lowered to the LLVMIR dialect, this form emits llvm.intr.fma, which
is guaranteed to lower to actual fma instructions on x86.
An optional kind attribute may be specified to be: add/mul/minsi
/minui/maxsi/maxui/and/or/xor for integers, and add/mul
/minnumf/maxnumf/minimumf/maximumf for floats. The default is
add.
Example:
%2 = vector.outerproduct %0, %1: vector<4xf32>, vector<8xf32>
return %2: vector<4x8xf32>
%3 = vector.outerproduct %0, %1, %2:
vector<4xf32>, vector<8xf32>, vector<4x8xf32>
return %3: vector<4x8xf32>
%4 = vector.outerproduct %0, %1, %2 {kind = #vector.kind<maxnumf>}:
vector<4xf32>, vector<8xf32>, vector<4x8xf32>
return %3: vector<4x8xf32>
%6 = vector.outerproduct %4, %5: vector<10xf32>, f32
return %6: vector<10xf32>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, MaskableOpInterface, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
kind | ::mlir::vector::CombiningKindAttr | Kind of combining function for contractions and reductionsEnum cases:
|
Operands: ¶
| Operand | Description |
|---|---|
lhs | vector of any type values |
rhs | any type |
acc | vector of any type values |
Results: ¶
| Result | Description |
|---|---|
| «unnamed» | vector of any type values |
vector.print (vector::PrintOp) ¶
Print operation (for testing and debugging)
Syntax:
operation ::= `vector.print` ($source^ `:` type($source))?
oilist(
`str` $stringLiteral
| `punctuation` $punctuation)
attr-dict
Prints the source vector (or scalar) to stdout in a human-readable format (for testing and debugging). No return value.
Example:
%v = arith.constant dense<0.0> : vector<4xf32>
vector.print %v : vector<4xf32>
When lowered to LLVM, the vector print is decomposed into elementary printing method calls that at runtime will yield:
( 0.0, 0.0, 0.0, 0.0 )
This is printed to stdout via a small runtime support library, which only needs to provide a few printing methods (single value for all data types, opening/closing bracket, comma, newline).
By default vector.print adds a newline after the vector, but this can be
controlled by the punctuation attribute. For example, to print a comma
after instead do:
vector.print %v : vector<4xf32> punctuation <comma>
Note that it is possible to use the punctuation attribute alone. The following will print a single newline:
vector.print punctuation <newline>
Additionally, to aid with debugging and testing vector.print can also
print constant strings:
vector.print str "Hello, World!"
Interfaces: MemoryEffectOpInterface (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{MemoryEffects::Write on ::mlir::SideEffects::DefaultResource}
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
punctuation | ::mlir::vector::PrintPunctuationAttr | Punctuation for separating vectors or vector elementsEnum cases:
|
stringLiteral | ::mlir::StringAttr | An Attribute containing a string |
Operands: ¶
| Operand | Description |
|---|---|
source |
vector.reduction (vector::ReductionOp) ¶
Reduction operation
Syntax:
operation ::= `vector.reduction` $kind `,` $vector (`,` $acc^)? (`fastmath` `` $fastmath^)? attr-dict `:` type($vector) `into` type($dest)
Reduces an 1-D vector “horizontally” into a scalar using the given
operation: add/mul/minsi/minui/maxsi/maxui/and/or/xor for
integers, and add/mul/minnumf/maxnumf/minimumf/maximumf for
floats. Reductions also allow an optional fused accumulator.
Note that these operations are restricted to 1-D vectors to remain close to the corresponding LLVM intrinsics:
http://llvm.org/docs/LangRef.html#vector-reduction-intrinsics
Example:
%1 = vector.reduction <add>, %0 : vector<16xf32> into f32
%3 = vector.reduction <xor>, %2 : vector<4xi32> into i32
%4 = vector.reduction <mul>, %0, %1 : vector<16xf32> into f32
Traits: AlwaysSpeculatableImplTrait
Interfaces: ArithFastMathInterface, ConditionallySpeculatable, MaskableOpInterface, NoMemoryEffect (MemoryEffectOpInterface), VectorUnrollOpInterface
Effects: MemoryEffects::Effect{}
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
kind | ::mlir::vector::CombiningKindAttr | Kind of combining function for contractions and reductionsEnum cases:
|
fastmath | ::mlir::arith::FastMathFlagsAttr | Floating point fast math flagsEnum cases:
|
Operands: ¶
| Operand | Description |
|---|---|
vector | vector of any type values |
acc | any type |
Results: ¶
| Result | Description |
|---|---|
dest | any type |
vector.reshape (vector::ReshapeOp) ¶
Vector reshape operation
Syntax:
operation ::= `vector.reshape` $vector `,` `[` $input_shape `]` `,` `[` $output_shape `]` `,`
$fixed_vector_sizes attr-dict `:` type($vector) `to` type($result)
Reshapes its vector operand from ‘input_shape’ to ‘output_shape’ maintaining fixed vector dimension ‘fixed_vector_sizes’ on the innermost vector dimensions.
The parameters ‘input_shape’ and ‘output_shape’ represent valid data shapes across fixed vector shapes. For example, if a vector has a valid data shape [6] with fixed vector size [8], then the valid data elements are assumed to be stored at the beginning of the vector with the remaining vector elements undefined.
In the examples below, valid data elements are represented by an alphabetic character, and undefined data elements are represented by ‘-’.
Example
vector<1x8xf32> with valid data shape [6], fixed vector sizes [8]
input: [a, b, c, d, e, f]
layout map: (d0) -> (d0 floordiv 8, d0 mod 8)
vector layout: [a, b, c, d, e, f, -, -]
Example
vector<2x8xf32> with valid data shape [10], fixed vector sizes [8]
input: [a, b, c, d, e, f, g, h, i, j]
layout map: (d0) -> (d0 floordiv 8, d0 mod 8)
vector layout: [[a, b, c, d, e, f, g, h],
[i, j, -, -, -, -, -, -]]
Example
vector<2x2x2x3xf32> with valid data shape [3, 5], fixed vector sizes [2, 3]
input: [[a, b, c, d, e],
[f, g, h, i, j],
[k, l, m, n, o]]
layout map: (d0, d1) -> (d0 floordiv 3, d1 floordiv 5,
d0 mod 3, d1 mod 5)
vector layout: [[[[a, b, c],
[f, g, h]]
[[d, e, -],
[i, j, -]]],
[[[k, l, m],
[-, -, -]]
[[n, o, -],
[-, -, -]]]]
Example
%1 = vector.reshape %0, [%c3, %c6], [%c2, %c9], [4] : vector<3x2x4xf32> to vector<2x3x4xf32>
input: [[a, b, c, d, e, f],
[g, h, i, j, k, l],
[m, n, o, p, q, r]]
layout map: (d0, d1) -> (d0, d1 floordiv 4, d1 mod 4)
Input vector: [[[a, b, c, d], [e, f, -, -]], [[g, h, i, j], [k, l, -, -]], [[m, n, o, p], [q, r, -, -]]]
Output vector: [[[a, b, c, d], [e, f, g, h], [i, -, -, -]], [[j, k, l, m], [n, o, p, q], [r, -, -, -]]]
Traits: AlwaysSpeculatableImplTrait, AttrSizedOperandSegments
Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
fixed_vector_sizes | ::mlir::ArrayAttr | 64-bit integer array attribute |
Operands: ¶
| Operand | Description |
|---|---|
vector | vector of any type values |
input_shape | variadic of index |
output_shape | variadic of index |
Results: ¶
| Result | Description |
|---|---|
result | vector of any type values |
vector.scalable.extract (vector::ScalableExtractOp) ¶
Extract subvector from scalable vector operation
Syntax:
operation ::= `vector.scalable.extract` $source `[` $pos `]` attr-dict `:` type($res) `from` type($source)
Takes rank-1 source vector and a position pos within the source
vector, and extracts a subvector starting from that position.
The extraction position must be a multiple of the minimum size of the result vector. For the operation to be well defined, the destination vector must fit within the source vector from the specified position. Since the source vector is scalable and its runtime length is unknown, the validity of the operation can’t be verified nor guaranteed at compile time.
Example:
%1 = vector.scalable.extract %0[8] : vector<4xf32> from vector<[8]xf32>
%3 = vector.scalable.extract %2[0] : vector<[4]xf32> from vector<[8]xf32>
Invalid example:
%1 = vector.scalable.extract %0[5] : vector<4xf32> from vector<[16]xf32>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
pos | ::mlir::IntegerAttr | 64-bit signless integer attribute |
Operands: ¶
| Operand | Description |
|---|---|
source | of ranks 1 |
Results: ¶
| Result | Description |
|---|---|
res | of ranks 1 |
vector.scalable.insert (vector::ScalableInsertOp) ¶
Insert subvector into scalable vector operation
Syntax:
operation ::= `vector.scalable.insert` $source `,` $dest `[` $pos `]` attr-dict `:` type($source) `into` type($dest)
This operations takes a rank-1 fixed-length or scalable subvector and
inserts it within the destination scalable vector starting from the
position specificed by pos. If the source vector is scalable, the
insertion position will be scaled by the runtime scaling factor of the
source subvector.
The insertion position must be a multiple of the minimum size of the source vector. For the operation to be well defined, the source vector must fit in the destination vector from the specified position. Since the destination vector is scalable and its runtime length is unknown, the validity of the operation can’t be verified nor guaranteed at compile time.
Example:
%2 = vector.scalable.insert %0, %1[8] : vector<4xf32> into vector<[16]xf32>
%5 = vector.scalable.insert %3, %4[0] : vector<8xf32> into vector<[4]xf32>
%8 = vector.scalable.insert %6, %7[0] : vector<[4]xf32> into vector<[8]xf32>
Invalid example:
%2 = vector.scalable.insert %0, %1[5] : vector<4xf32> into vector<[16]xf32>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
pos | ::mlir::IntegerAttr | 64-bit signless integer attribute |
Operands: ¶
| Operand | Description |
|---|---|
source | of ranks 1 |
dest | of ranks 1 |
Results: ¶
| Result | Description |
|---|---|
res | of ranks 1 |
vector.scan (vector::ScanOp) ¶
Scan operation
Syntax:
operation ::= `vector.scan` $kind `,` $source `,` $initial_value attr-dict `:` type($source) `,` type($initial_value)
Performs an inclusive/exclusive scan on an n-D vector along a single
dimension returning an n-D result vector using the given
operation (add/mul/minsi/minui/maxsi/maxui/and/or/xor for
integers, and add/mul/minnumf/maxnumf/minimumf/maximumf for
floats), and a specified value for the initial value. The operator returns
the result of scan as well as the result of the last reduction in the scan.
Example:
%1:2 = vector.scan <add>, %0, %acc {inclusive = false, reduction_dim = 1 : i64} :
vector<4x8x16x32xf32>, vector<4x16x32xf32>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
kind | ::mlir::vector::CombiningKindAttr | Kind of combining function for contractions and reductionsEnum cases:
|
reduction_dim | ::mlir::IntegerAttr | 64-bit signless integer attribute |
inclusive | ::mlir::BoolAttr | bool attribute |
Operands: ¶
| Operand | Description |
|---|---|
source | vector of any type values |
initial_value | vector of any type values |
Results: ¶
| Result | Description |
|---|---|
dest | vector of any type values |
accumulated_value | vector of any type values |
vector.scatter (vector::ScatterOp) ¶
Scatters elements from a vector into memory as defined by an index vector and a mask vector
Syntax:
operation ::= `vector.scatter` $base `[` $indices `]` `[` $index_vec `]` `,` $mask `,` $valueToStore attr-dict `:` type($base) `,` type($index_vec) `,` type($mask) `,` type($valueToStore)
The scatter operation stores elements from a 1-D vector into memory as defined by a base with indices and an additional 1-D index vector, but only if the corresponding bit in a 1-D mask vector is set. Otherwise, no action is taken for that element. Informally the semantics are:
if (mask[0]) base[index[0]] = value[0]
if (mask[1]) base[index[1]] = value[1]
etc.
If a mask bit is set and the corresponding index is out-of-bounds for the given base, the behavior is undefined. If a mask bit is not set, no value is stored regardless of the index, and the index is allowed to be out-of-bounds.
If the index vector contains two or more duplicate indices, the behavior is undefined. Underlying implementation may enforce strict sequential semantics. TODO: always enforce strict sequential semantics?
The scatter operation can be used directly where applicable, or can be used
during progressively lowering to bring other memory operations closer to
hardware ISA support for a scatter. The semantics of the operation closely
correspond to those of the llvm.masked.scatter
intrinsic.
Examples:
vector.scatter %base[%c0][%v], %mask, %value
: memref<?xf32>, vector<16xi32>, vector<16xi1>, vector<16xf32>
vector.scatter %base[%i, %j][%v], %mask, %value
: memref<16x16xf32>, vector<16xi32>, vector<16xi1>, vector<16xf32>
Operands: ¶
| Operand | Description |
|---|---|
base | memref of any type values |
indices | variadic of index |
index_vec | vector of integer or index values of ranks 1 |
mask | vector of 1-bit signless integer values of ranks 1 |
valueToStore | of ranks 1 |
vector.shape_cast (vector::ShapeCastOp) ¶
Shape_cast casts between vector shapes
Syntax:
operation ::= `vector.shape_cast` $source attr-dict `:` type($source) `to` type($result)
The shape_cast operation casts between an n-D source vector shape and a k-D result vector shape (the element type remains the same).
If reducing rank (n > k), result dimension sizes must be a product of contiguous source dimension sizes. If expanding rank (n < k), source dimensions must factor into a contiguous sequence of destination dimension sizes. Each source dim is expanded (or contiguous sequence of source dims combined) in source dimension list order (i.e. 0 <= i < n), to produce a contiguous sequence of result dims (or a single result dim), in result dimension list order (i.e. 0 <= j < k). The product of all source dimension sizes and all result dimension sizes must match.
It is currently assumed that this operation does not require moving data, and that it will be folded away before lowering vector operations.
There is an exception to the folding expectation when targeting llvm.intr.matrix operations. We need a type conversion back and forth from a 2-D MLIR vector to a 1-D flattened LLVM vector.shape_cast lowering to LLVM is supported in that particular case, for now.
Example:
// Example casting to a lower vector rank.
%1 = vector.shape_cast %0 : vector<5x1x4x3xf32> to vector<20x3xf32>
// Example casting to a higher vector rank.
%3 = vector.shape_cast %2 : vector<10x12x8xf32> to vector<5x2x3x4x8xf32>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Operands: ¶
| Operand | Description |
|---|---|
source | vector of any type values |
Results: ¶
| Result | Description |
|---|---|
result | vector of any type values |
vector.shuffle (vector::ShuffleOp) ¶
Shuffle operation
Syntax:
operation ::= `vector.shuffle` operands $mask attr-dict `:` type(operands)
The shuffle operation constructs a permutation (or duplication) of elements from two input vectors, returning a vector with the same element type as the input and a length that is the same as the shuffle mask. The two input vectors must have the same element type, same rank , and trailing dimension sizes and shuffles their values in the leading dimension (which may differ in size) according to the given mask. The legality rules are:
- the two operands must have the same element type as the result
- Either, the two operands and the result must have the same rank and trailing dimension sizes, viz. given two k-D operands v1 : <s_1 x s_2 x .. x s_k x type> and v2 : <t_1 x t_2 x .. x t_k x type> we have s_i = t_i for all 1 < i <= k
- Or, the two operands must be 0-D vectors and the result is a 1-D vector.
- the mask length equals the leading dimension size of the result
- numbering the input vector indices left to right across the operands, all mask values must be within range, viz. given two k-D operands v1 and v2 above, all mask values are in the range [0,s_1+t_1)
Note, scalable vectors are not supported.
Example:
%0 = vector.shuffle %a, %b[0, 3]
: vector<2xf32>, vector<2xf32> ; yields vector<2xf32>
%1 = vector.shuffle %c, %b[0, 1, 2]
: vector<2x16xf32>, vector<1x16xf32> ; yields vector<3x16xf32>
%2 = vector.shuffle %a, %b[3, 2, 1, 0]
: vector<2xf32>, vector<2xf32> ; yields vector<4xf32>
%3 = vector.shuffle %a, %b[0, 1]
: vector<f32>, vector<f32> ; yields vector<2xf32>
Traits: AlwaysSpeculatableImplTrait, InferTypeOpAdaptor
Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
mask | ::mlir::ArrayAttr | 64-bit integer array attribute |
Operands: ¶
| Operand | Description |
|---|---|
v1 | fixed-length vector of any type values |
v2 | fixed-length vector of any type values |
Results: ¶
| Result | Description |
|---|---|
vector | vector of any type values |
vector.splat (vector::SplatOp) ¶
Vector splat or broadcast operation
Syntax:
operation ::= `vector.splat` $input attr-dict `:` type($aggregate)
Broadcast the operand to all elements of the result vector. The operand is required to be of integer/index/float type.
Example:
%s = arith.constant 10.1 : f32
%t = vector.splat %s : vector<8x16xi32>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Operands: ¶
| Operand | Description |
|---|---|
input | integer/index/float type |
Results: ¶
| Result | Description |
|---|---|
aggregate | vector of any type values |
vector.step (vector::StepOp) ¶
A linear sequence of values from 0 to N
Syntax:
operation ::= `vector.step` attr-dict `:` type($result)
A step operation produces an index vector, i.e. a 1-D vector of values of
index type that represents a linear sequence from 0 to N-1, where N is the
number of elements in the result vector.
Supports fixed-width and scalable vectors.
Examples:
%0 = vector.step : vector<4xindex> ; [0, 1, 2, 3]
%1 = vector.step : vector<[4]xindex> ; [0, 1, .., <vscale * 4 - 1>]
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)
Effects: MemoryEffects::Effect{}
Results: ¶
| Result | Description |
|---|---|
result | vector of index values of ranks 1 |
vector.store (vector::StoreOp) ¶
Writes an n-D vector to an n-D slice of memory
Syntax:
operation ::= `vector.store` $valueToStore `,` $base `[` $indices `]` attr-dict `:` type($base) `,` type($valueToStore)
The ‘vector.store’ operation writes an n-D vector to an n-D slice of memory. It takes the vector value to be stored, a ‘base’ memref and an index for each memref dimension. The ‘base’ memref and indices determine the start memory address from which to write. Each index provides an offset for each memref dimension based on the element type of the memref. The shape of the vector value to store determines the shape of the slice written from the start memory address. The elements along each dimension of the slice are strided by the memref strides. Only unit strides are allowed along the most minor memref dimension. These constraints guarantee that elements written along the first dimension of the slice are contiguous in memory.
The memref element type can be a scalar or a vector type. If the memref element type is a scalar, it should match the element type of the value to store. If the memref element type is vector, it should match the type of the value to store.
Example: 0-D vector store on a scalar memref.
vector.store %valueToStore, %memref[%i, %j] : memref<200x100xf32>, vector<f32>
Example: 1-D vector store on a scalar memref.
vector.store %valueToStore, %memref[%i, %j] : memref<200x100xf32>, vector<8xf32>
Example: 1-D vector store on a vector memref.
vector.store %valueToStore, %memref[%i, %j] : memref<200x100xvector<8xf32>>, vector<8xf32>
Example: 2-D vector store on a scalar memref.
vector.store %valueToStore, %memref[%i, %j] : memref<200x100xf32>, vector<4x8xf32>
Example: 2-D vector store on a vector memref.
vector.store %valueToStore, %memref[%i, %j] : memref<200x100xvector<4x8xf32>>, vector<4x8xf32>
Representation-wise, the ‘vector.store’ operation permits out-of-bounds writes. Support and implementation of out-of-bounds vector stores are target-specific. No assumptions should be made on the memory written out of bounds. Not all targets may support out-of-bounds vector stores.
Example: Potential out-of-bounds vector store.
vector.store %valueToStore, %memref[%index] : memref<?xf32>, vector<8xf32>
Example: Explicit out-of-bounds vector store.
vector.store %valueToStore, %memref[%c0] : memref<7xf32>, vector<8xf32>
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
nontemporal | ::mlir::BoolAttr | bool attribute |
Operands: ¶
| Operand | Description |
|---|---|
valueToStore | vector of any type values |
base | memref of any type values |
indices | variadic of index |
vector.transfer_read (vector::TransferReadOp) ¶
Reads a supervector from memory into an SSA vector value.
The vector.transfer_read op performs a read from a slice within a
MemRef or a Ranked
Tensor supplied as its first operand
into a
vector of the same base elemental type.
A memref/tensor operand with vector element type, must have its vector element type match a suffix (shape and element type) of the vector (e.g. memref<3x2x6x4x3xf32>, vector<1x1x4x3xf32>).
The slice is further defined by a full-rank index within the MemRef/Tensor,
supplied as the operands [1 .. 1 + rank(memref/tensor)) that defines the
starting point of the transfer (e.g. %A[%i0, %i1, %i2]).
The permutation_map attribute is an affine-map which specifies the transposition on the slice to match the vector shape. The permutation map may be implicit and omitted from parsing and printing if it is the canonical minor identity map (i.e. if it does not permute or broadcast any dimension).
The size of the slice is specified by the size of the vector, given as the return type.
An SSA value padding of the same elemental type as the MemRef/Tensor is
provided to specify a fallback value in the case of out-of-bounds accesses
and/or masking.
An optional SSA value mask may be specified to mask out elements read from
the MemRef/Tensor. The mask type is an i1 vector with a shape that
matches how elements are read from the MemRef/Tensor, before any
permutation or broadcasting. Elements whose corresponding mask element is
0 are masked out and replaced with padding.
For every vector dimension, the boolean array attribute in_bounds
specifies if the transfer is guaranteed to be within the source bounds. If
set to “false”, accesses (including the starting point) may run
out-of-bounds along the respective vector dimension as the index increases.
Non-vector and broadcast dimensions must always be in-bounds. The
in_bounds array length has to be equal to the vector rank. This attribute
has a default value: false (i.e. “out-of-bounds”). When skipped in the
textual IR, the default value is assumed. Similarly, the OP printer will
omit this attribute when all dimensions are out-of-bounds (i.e. the default
value is used).
A vector.transfer_read can be lowered to a simple load if all dimensions
are specified to be within bounds and no mask was specified.
This operation is called ‘read’ by opposition to ’load’ because the
super-vector granularity is generally not representable with a single
hardware register. A vector.transfer_read is thus a mid-level abstraction
that supports super-vectorization with non-effecting padding for full-tile
only operations.
More precisely, let’s dive deeper into the permutation_map for the following MLIR:
vector.transfer_read %A[%expr1, %expr2, %expr3, %expr4]
{ permutation_map : (d0,d1,d2,d3) -> (d2,0,d0) } :
memref<?x?x?x?xf32>, vector<3x4x5xf32>
This operation always reads a slice starting at %A[%expr1, %expr2, %expr3, %expr4]. The size of the slice can be inferred from the resulting vector
shape and walking back through the permutation map: 3 along d2 and 5 along
d0, so the slice is: %A[%expr1 : %expr1 + 5, %expr2, %expr3:%expr3 + 3, %expr4]
That slice needs to be read into a vector<3x4x5xf32>. Since the
permutation map is not full rank, there must be a broadcast along vector
dimension 1.
A notional lowering of vector.transfer_read could generate code resembling:
// %expr1, %expr2, %expr3, %expr4 defined before this point
// alloc a temporary buffer for performing the "gather" of the slice.
%tmp = memref.alloc() : memref<vector<3x4x5xf32>>
for %i = 0 to 3 {
affine.for %j = 0 to 4 {
affine.for %k = 0 to 5 {
// Note that this load does not involve %j.
%a = load %A[%expr1 + %k, %expr2, %expr3 + %i, %expr4] : memref<?x?x?x?xf32>
// Update the temporary gathered slice with the individual element
%slice = memref.load %tmp : memref<vector<3x4x5xf32>> -> vector<3x4x5xf32>
%updated = vector.insert %a, %slice[%i, %j, %k] : f32 into vector<3x4x5xf32>
memref.store %updated, %tmp : memref<vector<3x4x5xf32>>
}}}
// At this point we gathered the elements from the original
// memref into the desired vector layout, stored in the `%tmp` allocation.
%vec = memref.load %tmp : memref<vector<3x4x5xf32>> -> vector<3x4x5xf32>
On a GPU one could then map i, j, k to blocks and threads. Notice that
the temporary storage footprint could conceptually be only 3 * 5 values but
3 * 4 * 5 values are actually transferred between %A and %tmp.
Alternatively, if a notional vector broadcast operation were available, we
could avoid the loop on %j and the lowered code would resemble:
// %expr1, %expr2, %expr3, %expr4 defined before this point
%tmp = memref.alloc() : memref<vector<3x4x5xf32>>
for %i = 0 to 3 {
affine.for %k = 0 to 5 {
%a = load %A[%expr1 + %k, %expr2, %expr3 + %i, %expr4] : memref<?x?x?x?xf32>
%slice = memref.load %tmp : memref<vector<3x4x5xf32>> -> vector<3x4x5xf32>
// Here we only store to the first element in dimension one
%updated = vector.insert %a, %slice[%i, 0, %k] : f32 into vector<3x4x5xf32>
memref.store %updated, %tmp : memref<vector<3x4x5xf32>>
}}
// At this point we gathered the elements from the original
// memref into the desired vector layout, stored in the `%tmp` allocation.
// However we haven't replicated them alongside the first dimension, we need
// to broadcast now.
%partialVec = load %tmp : memref<vector<3x4x5xf32>> -> vector<3x4x5xf32>
%vec = broadcast %tmpvec, 1 : vector<3x4x5xf32>
where broadcast broadcasts from element 0 to all others along the
specified dimension. This time, the number of loaded element is 3 * 5
values.
An additional 1 broadcast is required. On a GPU this broadcast could be
implemented using a warp-shuffle if loop j were mapped to threadIdx.x.
Syntax
operation ::= ssa-id `=` `vector.transfer_read` ssa-use-list
`{` attribute-entry `} :` memref-type `,` vector-type
Example:
// Read the slice `%A[%i0, %i1:%i1+256, %i2:%i2+32]` into vector<32x256xf32>
// and pad with %f0 to handle the boundary case:
%f0 = arith.constant 0.0f : f32
affine.for %i0 = 0 to %0 {
affine.for %i1 = 0 to %1 step 256 {
affine.for %i2 = 0 to %2 step 32 {
%v = vector.transfer_read %A[%i0, %i1, %i2], (%f0)
{permutation_map: (d0, d1, d2) -> (d2, d1)} :
memref<?x?x?xf32>, vector<32x256xf32>
}}}
// or equivalently (rewrite with vector.transpose)
%f0 = arith.constant 0.0f : f32
affine.for %i0 = 0 to %0 {
affine.for %i1 = 0 to %1 step 256 {
affine.for %i2 = 0 to %2 step 32 {
%v0 = vector.transfer_read %A[%i0, %i1, %i2], (%f0)
{permutation_map: (d0, d1, d2) -> (d1, d2)} :
memref<?x?x?xf32>, vector<256x32xf32>
%v = vector.transpose %v0, [1, 0] :
vector<256x32xf32> to vector<32x256f32>
}}}
// Read the slice `%A[%i0, %i1]` (i.e. the element `%A[%i0, %i1]`) into
// vector<128xf32>. The underlying implementation will require a 1-D vector
// broadcast:
affine.for %i0 = 0 to %0 {
affine.for %i1 = 0 to %1 {
%3 = vector.transfer_read %A[%i0, %i1]
{permutation_map: (d0, d1) -> (0)} :
memref<?x?xf32>, vector<128xf32>
}
}
// Read from a memref with vector element type.
%4 = vector.transfer_read %arg1[%c3, %c3], %vf0
{permutation_map = (d0, d1)->(d0, d1)}
: memref<?x?xvector<4x3xf32>>, vector<1x1x4x3xf32>
// Read from a tensor with vector element type.
%4 = vector.transfer_read %arg1[%c3, %c3], %vf0
{permutation_map = (d0, d1)->(d0, d1)}
: tensor<?x?xvector<4x3xf32>>, vector<1x1x4x3xf32>
// Special encoding for 0-d transfer with 0-d tensor/memref, vector shape
// {1} and permutation_map () -> (0).
%0 = vector.transfer_read %arg0[], %f0 {permutation_map = affine_map<()->(0)>} :
tensor<f32>, vector<1xf32>
Traits: AttrSizedOperandSegments
Interfaces: DestinationStyleOpInterface, MaskableOpInterface, MemoryEffectOpInterface, VectorTransferOpInterface, VectorUnrollOpInterface
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
permutation_map | ::mlir::AffineMapAttr | AffineMap attribute |
in_bounds | ::mlir::ArrayAttr | 1-bit boolean array attribute |
Operands: ¶
| Operand | Description |
|---|---|
source | shaped of any type values |
indices | variadic of index |
padding | any type |
mask | vector of 1-bit signless integer values |
Results: ¶
| Result | Description |
|---|---|
vector | vector of any type values |
vector.transfer_write (vector::TransferWriteOp) ¶
The vector.transfer_write op writes a supervector to memory.
The vector.transfer_write op performs a write from a
vector, supplied as its first operand, into a
slice within a
MemRef or a Ranked
Tensor of the same base elemental type,
supplied as its second operand.
A vector memref/tensor operand must have its vector element type match a suffix (shape and element type) of the vector (e.g. memref<3x2x6x4x3xf32>, vector<1x1x4x3xf32>). If the operand is a tensor, the operation returns a new tensor of the same type.
The slice is further defined by a full-rank index within the MemRef/Tensor,
supplied as the operands [2 .. 2 + rank(memref/tensor)) that defines the
starting point of the transfer (e.g. %A[%i0, %i1, %i2, %i3]).
The permutation_map
attribute is an
affine-map which specifies the transposition on the
slice to match the vector shape. The permutation map may be implicit and
omitted from parsing and printing if it is the canonical minor identity map
(i.e. if it does not permute any dimension). In contrast to transfer_read,
write ops cannot have broadcast dimensions.
The size of the slice is specified by the size of the vector.
An optional SSA value mask may be specified to mask out elements written
to the MemRef/Tensor. The mask type is an i1 vector with a shape that
matches how elements are written into the MemRef/Tensor, after applying
any permutation. Elements whose corresponding mask element is 0 are
masked out.
For every vector dimension, the boolean array attribute in_bounds
specifies if the transfer is guaranteed to be within the source bounds. If
set to “false”, accesses (including the starting point) may run
out-of-bounds along the respective vector dimension as the index increases.
Non-vector and broadcast dimensions must always be in-bounds. The
in_bounds array length has to be equal to the vector rank. This attribute
has a default value: false (i.e. “out-of-bounds”). When skipped in the
textual IR, the default value is assumed. Similarly, the OP printer will
omit this attribute when all dimensions are out-of-bounds (i.e. the default
value is used).
A vector.transfer_write can be lowered to a simple store if all
dimensions are specified to be within bounds and no mask was specified.
This operation is called ‘write’ by opposition to ‘store’ because the
super-vector granularity is generally not representable with a single
hardware register. A vector.transfer_write is thus a
mid-level abstraction that supports super-vectorization with non-effecting
padding for full-tile-only code. It is the responsibility of
vector.transfer_write’s implementation to ensure the memory writes are
valid. Different lowerings may be pertinent depending on the hardware
support.
Example:
// write vector<16x32x64xf32> into the slice
// `%A[%i0, %i1:%i1+32, %i2:%i2+64, %i3:%i3+16]`:
for %i0 = 0 to %0 {
affine.for %i1 = 0 to %1 step 32 {
affine.for %i2 = 0 to %2 step 64 {
affine.for %i3 = 0 to %3 step 16 {
%val = `ssa-value` : vector<16x32x64xf32>
vector.transfer_write %val, %A[%i0, %i1, %i2, %i3]
{permutation_map: (d0, d1, d2, d3) -> (d3, d1, d2)} :
vector<16x32x64xf32>, memref<?x?x?x?xf32>
}}}}
// or equivalently (rewrite with vector.transpose)
for %i0 = 0 to %0 {
affine.for %i1 = 0 to %1 step 32 {
affine.for %i2 = 0 to %2 step 64 {
affine.for %i3 = 0 to %3 step 16 {
%val = `ssa-value` : vector<16x32x64xf32>
%valt = vector.transpose %val, [1, 2, 0] :
vector<16x32x64xf32> -> vector<32x64x16xf32>
vector.transfer_write %valt, %A[%i0, %i1, %i2, %i3]
{permutation_map: (d0, d1, d2, d3) -> (d1, d2, d3)} :
vector<32x64x16xf32>, memref<?x?x?x?xf32>
}}}}
// write to a memref with vector element type.
vector.transfer_write %4, %arg1[%c3, %c3]
{permutation_map = (d0, d1)->(d0, d1)}
: vector<1x1x4x3xf32>, memref<?x?xvector<4x3xf32>>
// return a tensor where the vector is inserted into the source tensor.
%5 = vector.transfer_write %4, %arg1[%c3, %c3]
{permutation_map = (d0, d1)->(d0, d1)}
: vector<1x1x4x3xf32>, tensor<?x?xvector<4x3xf32>>
// Special encoding for 0-d transfer with 0-d tensor/memref, vector shape
// {1} and permutation_map () -> (0).
%1 = vector.transfer_write %0, %arg0[] {permutation_map = affine_map<()->(0)>} :
vector<1xf32>, tensor<f32>
Traits: AttrSizedOperandSegments
Interfaces: DestinationStyleOpInterface, MaskableOpInterface, MemoryEffectOpInterface, VectorTransferOpInterface, VectorUnrollOpInterface
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
permutation_map | ::mlir::AffineMapAttr | AffineMap attribute |
in_bounds | ::mlir::ArrayAttr | 1-bit boolean array attribute |
Operands: ¶
| Operand | Description |
|---|---|
vector | vector of any type values |
source | shaped of any type values |
indices | variadic of index |
mask | vector of 1-bit signless integer values |
Results: ¶
| Result | Description |
|---|---|
result | ranked tensor of any type values |
vector.transpose (vector::TransposeOp) ¶
Vector transpose operation
Syntax:
operation ::= `vector.transpose` $vector `,` $permutation attr-dict `:` type($vector) `to` type($result)
Takes a n-D vector and returns the transposed n-D vector defined by the permutation of ranks in the n-sized integer array attribute (in case of 0-D vectors the array attribute must be empty).
In the operation
%1 = vector.transpose %0, [i_1, .., i_n]
: vector<d_1 x .. x d_n x f32>
to vector<d_trans[0] x .. x d_trans[n-1] x f32>
the permutation array [i_1, .., i_n] must be a permutation of [0, .., n-1].
Example:
%1 = vector.transpose %0, [1, 0] : vector<2x3xf32> to vector<3x2xf32>
[ [a, b, c], [ [a, d],
[d, e, f] ] -> [b, e],
[c, f] ]
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface), VectorUnrollOpInterface
Effects: MemoryEffects::Effect{}
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
permutation | ::mlir::DenseI64ArrayAttr | i64 dense array attribute |
Operands: ¶
| Operand | Description |
|---|---|
vector | vector of any type values |
Results: ¶
| Result | Description |
|---|---|
result | vector of any type values |
vector.type_cast (vector::TypeCastOp) ¶
Type_cast op converts a scalar memref to a vector memref
Syntax:
operation ::= `vector.type_cast` $memref attr-dict `:` type($memref) `to` type($result)
Performs a conversion from a memref with scalar element to a memref with a
single vector element, copying the shape of the memref to the vector. This
is the minimal viable operation that is required to makeke
super-vectorization operational. It can be seen as a special case of the
view operation but scoped in the super-vectorization context.
Example:
%A = memref.alloc() : memref<5x4x3xf32>
%VA = vector.type_cast %A : memref<5x4x3xf32> to memref<vector<5x4x3xf32>>
Traits: AlwaysSpeculatableImplTrait
Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface), ViewLikeOpInterface
Effects: MemoryEffects::Effect{}
Operands: ¶
| Operand | Description |
|---|---|
memref | statically shaped memref of any type values |
Results: ¶
| Result | Description |
|---|---|
result | memref of any type values |
vector.warp_execute_on_lane_0 (vector::WarpExecuteOnLane0Op) ¶
Executes operations in the associated region on thread #0 of aSPMD program
warp_execute_on_lane_0 is an operation used to bridge the gap between
vector programming and SPMD programming model like GPU SIMT. It allows to
trivially convert a region of vector code meant to run on a multiple threads
into a valid SPMD region and then allows incremental transformation to
distribute vector operations on the threads.
Any code present in the region would only be executed on first thread/lane
based on the laneid operand. The laneid operand is an integer ID between
[0, warp_size). The warp_size attribute indicates the number of lanes in
a warp.
Operands are vector values distributed on all lanes that may be used by the single lane execution. The matching region argument is a vector of all the values of those lanes available to the single active lane. The distributed dimension is implicit based on the shape of the operand and argument. the properties of the distribution may be described by extra attributes (e.g. affine map).
Return values are distributed on all lanes using laneId as index. The vector is distributed based on the shape ratio between the vector type of the yield and the result type. If the shapes are the same this means the value is broadcasted to all lanes. In the future the distribution can be made more explicit using affine_maps and will support having multiple Ids.
Therefore the warp_execute_on_lane_0 operations allow to implicitly copy
between lane0 and the lanes of the warp. When distributing a vector
from lane0 to all the lanes, the data are distributed in a block cyclic way.
For exemple vector<64xf32> gets distributed on 32 threads and map to
vector<2xf32> where thread 0 contains vector[0] and vector[1].
During lowering values passed as operands and return value need to be visible to different lanes within the warp. This would usually be done by going through memory.
The region is not isolated from above. For values coming from the parent region not going through operands only the lane 0 value will be accesible so it generally only make sense for uniform values.
Example:
// Execute in parallel on all threads/lanes.
vector.warp_execute_on_lane_0 (%laneid)[32] {
// Serial code running only on thread/lane 0.
...
}
// Execute in parallel on all threads/lanes.
This may be lowered to an scf.if region as below:
// Execute in parallel on all threads/lanes.
%cnd = arith.cmpi eq, %laneid, %c0 : index
scf.if %cnd {
// Serial code running only on thread/lane 0.
...
}
// Execute in parallel on all threads/lanes.
When the region has operands and/or return values:
// Execute in parallel on all threads/lanes.
%0 = vector.warp_execute_on_lane_0(%laneid)[32]
args(%v0 : vector<4xi32>) -> (vector<1xf32>) {
^bb0(%arg0 : vector<128xi32>) :
// Serial code running only on thread/lane 0.
...
vector.yield %1 : vector<32xf32>
}
// Execute in parallel on all threads/lanes.
values at the region boundary would go through memory:
// Execute in parallel on all threads/lanes.
...
// Store the data from each thread into memory and Synchronization.
%tmp0 = memreg.alloc() : memref<128xf32>
%tmp1 = memreg.alloc() : memref<32xf32>
%cnd = arith.cmpi eq, %laneid, %c0 : index
vector.store %v0, %tmp0[%laneid] : memref<128xf32>, vector<4xf32>
some_synchronization_primitive
scf.if %cnd {
// Serialized code running only on thread 0.
// Load the data from all the threads into a register from thread 0. This
// allow threads 0 to access data from all the threads.
%arg0 = vector.load %tmp0[%c0] : memref<128xf32>, vector<128xf32>
...
// Store the data from thread 0 into memory.
vector.store %1, %tmp1[%c0] : memref<32xf32>, vector<32xf32>
}
// Synchronization and load the data in a block cyclic way so that the
// vector is distributed on all threads.
some_synchronization_primitive
%0 = vector.load %tmp1[%laneid] : memref<32xf32>, vector<32xf32>
// Execute in parallel on all threads/lanes.
Traits: RecursiveMemoryEffects, SingleBlockImplicitTerminator<vector::YieldOp>, SingleBlock
Interfaces: RegionBranchOpInterface
Attributes: ¶
| Attribute | MLIR Type | Description |
|---|---|---|
warp_size | ::mlir::IntegerAttr | 64-bit signless integer attribute |
Operands: ¶
| Operand | Description |
|---|---|
laneid | index |
args | variadic of any type |
Results: ¶
| Result | Description |
|---|---|
results | variadic of any type |
vector.yield (vector::YieldOp) ¶
Terminates and yields values from vector regions.
Syntax:
operation ::= `vector.yield` attr-dict ($operands^ `:` type($operands))?
“vector.yield” yields an SSA value from the Vector dialect op region and terminates the regions. The semantics of how the values are yielded is defined by the parent operation. If “vector.yield” has any operands, the operands must correspond to the parent operation’s results. If the parent operation defines no value the vector.yield may be omitted when printing the region.
Traits: AlwaysSpeculatableImplTrait, ReturnLike, Terminator
Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface), RegionBranchTerminatorOpInterface
Effects: MemoryEffects::Effect{}
Operands: ¶
| Operand | Description |
|---|---|
operands | variadic of any type |
 MLIR
MLIR