'vector' Dialect

MLIR supports multi-dimensional vector types and custom operations on those types. A generic, retargetable, higher-order vector type (n-D with n > 1) is a structured type, that carries semantic information useful for transformations. This document discusses retargetable abstractions that exist in MLIR today and operate on ssa-values of type vector along with pattern rewrites and lowerings that enable targeting specific instructions on concrete targets. These abstractions serve to separate concerns between operations on memref (a.k.a buffers) and operations on vector values. This is not a new proposal but rather a textual documentation of existing MLIR components along with a rationale.

Positioning in the Codegen Infrastructure ¶

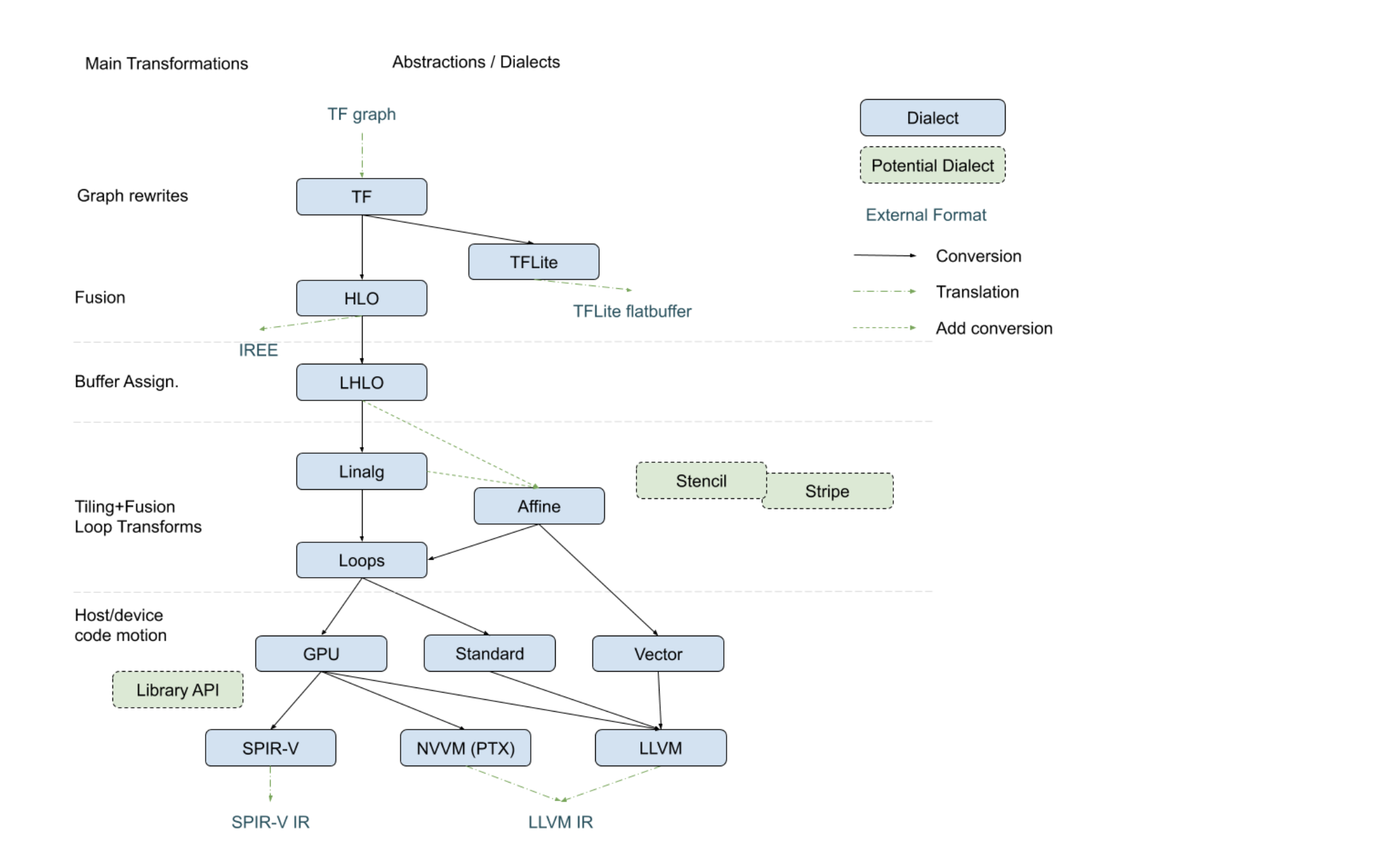
The following diagram, recently presented with the StructuredOps abstractions, captures the current codegen paths implemented in MLIR in the various existing lowering paths.

The following diagram seeks to isolate vector dialects from the complexity of the codegen paths and focus on the payload-carrying ops that operate on std and vector types. This diagram is not to be taken as set in stone and representative of what exists today but rather illustrates the layering of abstractions in MLIR.

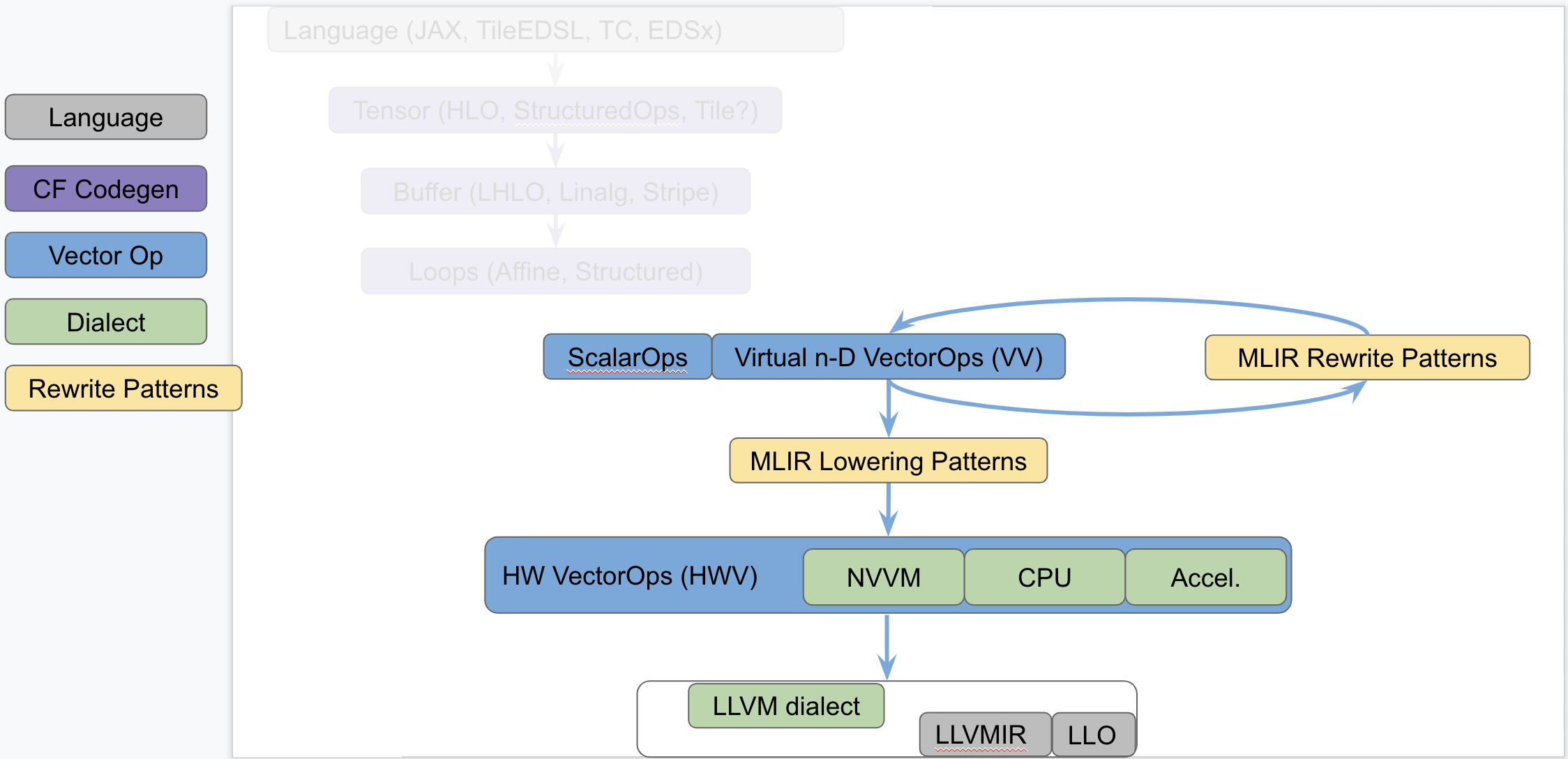
This  separates concerns related to (a) defining efficient operations on vector types from (b) program analyses + transformations on memref, loops and other types of structured ops (be they HLO, LHLO, Linalg or other ). Looking a bit forward in time, we can put a stake in the ground and venture that the higher level of vector-level primitives we build and target from codegen (or some user/language level), the simpler our task will be, the more complex patterns can be expressed and the better performance will be.

Components of a Generic Retargetable Vector-Level Dialect ¶

The existing MLIR vector-level dialects are related to the following bottom-up abstractions:

1. Representation in LLVMIR via data structures, instructions and intrinsics. This is referred to as the LLVM level.
2. Set of machine-specific operations and types that are built to translate almost 1-1 with the HW ISA. This is referred to as the Hardware Vector level; a.k.a HWV. For instance, we have (a) the NVVM dialect (for CUDA) with tensor core ops, (b) accelerator-specific dialects (internal), a potential (future) CPU dialect to capture LLVM intrinsics more closely and other dialects for specific hardware. Ideally this should be auto-generated as much as possible from the LLVM level.
3. Set of virtual, machine-agnostic, operations that are informed by costs at the HWV-level. This is referred to as the Virtual Vector level; a.k.a VV. This is the level that higher-level abstractions (codegen, automatic vectorization, potential vector language, …) targets.

The existing generic, retargetable, vector-level dialect is related to the following top-down rewrites and conversions:

1. MLIR Rewrite Patterns applied by the MLIR PatternRewrite infrastructure to progressively lower to implementations that match closer and closer to the HWV. Some patterns are “in-dialect” VV -> VV and some are conversions VV -> HWV.
2. Virtual Vector -> Hardware Vector lowering is specified as a set of MLIR lowering patterns that are specified manually for now.
3. Hardware Vector -> LLVM lowering is a mechanical process that is written manually at the moment and that should be automated, following the LLVM -> Hardware Vector ops generation as closely as possible.

Short Description of the Existing Infrastructure ¶

LLVM level ¶

On CPU, the n-D vector type currently lowers to !llvm<array<vector>>. More concretely,

• vector<4x8x128xf32> lowers to !llvm<[4 x [ 8 x < 128 x float >]]> (fixed-width vector), and
• vector<4x8x[128]xf32> lowers to !llvm<[4 x [ 8 x < vscale x 128 x float >]]> (scalable vector).

There are tradeoffs involved related to how one can access subvectors and how one uses llvm.extractelement, llvm.insertelement and llvm.shufflevector. The section on LLVM Lowering Tradeoffs offers a deeper dive into the current design choices and tradeoffs.

Note, while LLVM supports arrarys of scalable vectors, these are required to be fixed-width arrays of 1-D scalable vectors. This means scalable vectors with a non-trailing scalable dimension (e.g. vector<4x[8]x128xf32) are not convertible to LLVM.

Finally, MLIR takes the same view on scalable Vectors as LLVM (c.f. VectorType):

For scalable vectors, the total number of elements is a constant multiple (called vscale) of the specified number of elements; vscale is a positive integer that is unknown at compile time and the same hardware-dependent constant for all scalable vectors at run time. The size of a specific scalable vector type is thus constant within IR, even if the exact size in bytes cannot be determined until run time.

Hardware Vector Ops ¶

Hardware Vector Ops are implemented as one dialect per target. For internal hardware, we are auto-generating the specific HW dialects. For GPU, the NVVM dialect adds operations such as mma.sync, shfl and tests. For CPU things are somewhat in-flight because the abstraction is close to LLVMIR. The jury is still out on  whether a generic CPU dialect is concretely needed, but it seems reasonable to have the same levels of abstraction for all targets and perform cost-based lowering decisions in MLIR even for LLVM. Specialized CPU dialects that would capture specific features not well captured by LLVM peephole optimizations of on different types that core MLIR supports (e.g. Scalable Vectors) are welcome future extensions.

Virtual Vector Ops ¶

Some existing Arith and Vector Dialect on n-D vector types comprise:

// Produces a vector<3x7x8xf32>
%a = arith.addf %0, %1 : vector<3x7x8xf32>
// Produces a vector<3x7x8xf32>
%b = arith.mulf %0, %1 : vector<3x7x8xf32>
// Produces a vector<3x7x8xf32>
%c = vector.splat %1 : vector<3x7x8xf32>

%d = vector.extract %0[1]: vector<7x8xf32> from vector<3x7x8xf32>
%e = vector.extract %0[1, 5]: vector<8xf32> from vector<3x7x8xf32>
%f = vector.outerproduct %0, %1: vector<4xf32>, vector<8xf32>      // -> vector<4x8xf32>
%g = vector.outerproduct %0, %1, %2: vector<4xf32>, vector<8xf32>  // fma when adding %2

// Returns a slice of type vector<2x2x16xf32>
%h = vector.strided_slice %0
    {offsets = [2, 2], sizes = [2, 2], strides = [1, 1]}:
  vector<4x8x16xf32>

%i = vector.transfer_read %A[%0, %1]
    {permutation_map = (d0, d1) -> (d0)}:
  memref<7x?xf32>, vector<4xf32>

vector.transfer_write %f1, %A[%i0, %i1, %i2, %i3]
    {permutation_map = (d0, d1, d2, d3) -> (d3, d1, d0)} :
  vector<5x4x3xf32>, memref<?x?x?x?xf32>

The list of Vector is currently undergoing evolutions and is best kept track of by following the evolution of the VectorOps.td ODS file (markdown documentation is automatically generated locally when building and populates the Vector doc). Recent extensions are driven by concrete use cases of interest. A notable such use case is the vector.contract op which applies principles of the StructuredOps abstraction to vector types.

Virtual Vector Rewrite Patterns ¶

The following rewrite patterns exist at the VV->VV level:

1. The now retired MaterializeVector pass used to legalize ops on a coarse-grained virtual vector to a finer-grained virtual vector by unrolling. This has been rewritten as a retargetable unroll-and-jam pattern on vector ops and vector types.
2. The lowering of vector_transfer ops legalizes vector load/store ops to permuted loops over scalar load/stores. This should evolve to loops over vector load/stores + mask operations as they become available vector ops at the VV level.

The general direction is to add more Virtual Vector level ops and implement more useful VV -> VV rewrites as composable patterns that the PatternRewrite infrastructure can apply iteratively.

Virtual Vector to Hardware Vector Lowering ¶

For now, VV -> HWV are specified in C++ (see for instance the SplatOpLowering for n-D vectors or the VectorOuterProductOp lowering).

Simple conversion tests are available for the LLVM target starting from the Virtual Vector Level.

Rationale ¶

Hardware as vector Machines of Minimum Granularity ¶

Higher-dimensional vectors are ubiquitous in modern HPC hardware. One way to think about Generic Retargetable vector-Level Dialect is that it operates on vector types that are multiples of a “good” vector size so the HW can efficiently implement a set of high-level primitives (e.g. vector<8x8x8x16xf32> when HW vector size is say vector<4x8xf32>).

Some notable vector sizes of interest include:

1. CPU: vector<HW_vector_size * k>, vector<core_count * k’ x HW_vector_size * k> and vector<socket_count x core_count * k’ x HW_vector_size * k>
2. GPU: vector<warp_size * k>, vector<warp_size * k x float4> and vector<warp_size * k x 4 x 4 x 4> for tensor_core sizes,
3. Other accelerators: n-D vector as first-class citizens in the HW.

Depending on the target, ops on sizes that are not multiples of the HW vector size may either produce slow code (e.g. by going through LLVM legalization) or may not legalize at all (e.g. some unsupported accelerator X combination of ops and types).

Transformations Problems Avoided ¶

A vector<16x32x64xf32> virtual vector is a coarse-grained type that can be “unrolled” to HW-specific sizes. The multi-dimensional unrolling factors are carried in the IR by the vector type. After unrolling, traditional instruction-level scheduling can be run.

The following key transformations (along with the supporting analyses and structural constraints) are completely avoided by operating on a vector ssa-value abstraction:

1. Loop unroll and unroll-and-jam.
2. Loop and load-store restructuring for register reuse.
3. Load to store forwarding and Mem2reg.
4. Coarsening (raising) from finer-grained vector form.

Note that “unrolling” in the context of vectors corresponds to partial loop unroll-and-jam and not full unrolling. As a consequence this is expected to compose with SW pipelining where applicable and does not result in ICache blow up.

The Big Out-Of-Scope Piece: Automatic Vectorization ¶

One important piece not discussed here is automatic vectorization (automatically raising from scalar to n-D vector ops and types). The TL;DR is that when the first “super-vectorization” prototype was implemented, MLIR was nowhere near as mature as it is today. As we continue building more abstractions in VV -> HWV, there is an opportunity to revisit vectorization in MLIR.

Since this topic touches on codegen abstractions, it is technically out of the scope of this survey document but there is a lot to discuss in light of structured op type representations and how a vectorization transformation can be reused across dialects. In particular, MLIR allows the definition of dialects at arbitrary levels of granularity and lends itself favorably to progressive lowering. The argument can be made that automatic vectorization on a loops + ops abstraction is akin to raising structural information that has been lost. Instead, it is possible to revisit vectorization as simple pattern rewrites, provided the IR is in a suitable form. For instance, vectorizing a linalg.generic op whose semantics match a matmul can be done quite easily with a pattern. In fact this pattern is trivial to generalize to any type of contraction when targeting the vector.contract op, as well as to any field (+/*, min/+, max/+, or/and, logsumexp/+ …) . In other words, by operating on a higher level of generic abstractions than affine loops, non-trivial transformations become significantly simpler and composable at a finer granularity.

Irrespective of the existence of an auto-vectorizer, one can build a notional vector language based on the VectorOps dialect and build end-to-end models with expressing vectors in the IR directly and simple pattern-rewrites. EDSCs provide a simple way of driving such a notional language directly in C++.

Bikeshed Naming Discussion ¶

There are arguments against naming an n-D level of abstraction vector because most people associate it with 1-D vectors. On the other hand, vectors are first-class n-D values in MLIR. The alternative name Tile has been proposed, which conveys higher-D meaning. But it also is one of the most overloaded terms in compilers and hardware. For now, we generally use the n-D vector name and are open to better suggestions.

0D Vectors ¶

Vectors of dimension 0 (or 0-D vectors or 0D vectors) are allowed inside MLIR. For instance, a f32 vector containing one scalar can be denoted as vector<f32>. This is similar to the tensor<f32> type that is available in TensorFlow or the memref<f32> type that is available in MLIR.

Generally, a 0D vector can be interpreted as a scalar. The benefit of 0D vectors, tensors, and memrefs is that they make it easier to lower code from various frontends such as TensorFlow and make it easier to handle corner cases such as unrolling a loop from 1D to 0D.

LLVM Lowering Tradeoffs ¶

This section describes the tradeoffs involved in lowering the MLIR n-D vector type and operations on it to LLVM-IR. Putting aside the LLVM Matrix proposal for now, this assumes LLVM only has built-in support for 1-D vector. The relationship with the LLVM Matrix proposal is discussed at the end of this document.

LLVM instructions are prefixed by the llvm. dialect prefix (e.g. llvm.insertvalue). Such ops operate exclusively on 1-D vectors and aggregates following the LLVM LangRef. MLIR operations are prefixed by the vector. dialect prefix (e.g. vector.insertelement). Such ops operate exclusively on MLIR n-D vector types.

Alternatives For Lowering an n-D Vector Type to LLVM ¶

Consider a vector of rank n with static sizes {s_0, ... s_{n-1}} (i.e. an MLIR vector<s_0x...s_{n-1}xf32>). Lowering such an n-D MLIR vector type to an LLVM descriptor can be done by either:

1. Nested aggregate type of 1-D vector: !llvm."[s_0x[s_1x[...<s_{n-1}xf32>]]]"> in the MLIR LLVM dialect (current lowering in MLIR).
2. Flattening to a 1-D vector: !llvm<"(s_0*...*s_{n-1})xfloat"> in the MLIR LLVM dialect.
3. A mix of both.

There are multiple tradeoffs involved in choosing one or the other that we discuss. It is important to note that “a mix of both” immediately reduces to “nested aggregate type of 1-D vector” with a vector.cast %0: vector<4x8x16x32xf32> to vector<4x4096xf32> operation, that flattens the most “k” minor dimensions.

Constraints Inherited from LLVM (see LangRef) ¶

The first constraint was already mentioned: LLVM only supports 1-D vector types natively. Additional constraints are related to the difference in LLVM between vector and aggregate types:

Aggregate Types are a subset of derived types that can contain multiple member types. Arrays and structs are aggregate types. Vectors are not considered to be aggregate types.

This distinction is also reflected in some of the operations. For 1-D vectors, the operations llvm.extractelement, llvm.insertelement, and llvm.shufflevector apply, with direct support for dynamic indices. For n-D vectors with n>1, and thus aggregate types at LLVM level, the more restrictive operations llvm.extractvalue and llvm.insertvalue apply, which only accept static indices. There is no direct shuffling support for aggregate types.

The next sentence (cf. LangRef structure type) illustrates a recurrent tradeoff, also found in MLIR, between “value types” (subject to SSA use-def chains) and “memory types” (subject to aliasing and side-effects):

Structures in memory are accessed using ‘load’ and ‘store’ by getting a pointer to a field with the llvm.getelementptr instruction. Structures in registers are accessed using the llvm.extractvalue and llvm.insertvalue instructions.

When transposing this to MLIR, llvm.getelementptr works on pointers to n-D vectors in memory. For n-D, vectors values that live in registers we can use vector.extract and vector.insert which do not accept dynamic indices. Note that this is consistent with hardware considerations as discussed below.

An alternative is to use an LLVM 1-D vector type for which one can use llvm.extractelement, llvm.insertelement and llvm.shufflevector. These operations accept dynamic indices. The implication is that one has to use a flattened lowering of an MLIR n-D vector to an LLVM 1-D vector.

There are multiple tradeoffs involved that mix implications on the programming model, execution on actual HW and what is visible or hidden from codegen. They are discussed in the following sections.

Nested Aggregate ¶

Pros:

1. Natural encoding n-D vector -> (n-1)-D aggregate over 1-D vector.
2. No need for linearization / delinearization logic inserted everywhere.
3. llvm.insertvalue, llvm.extractvalue of (n-k)-D aggregate is natural.
4. llvm.insertelement, llvm.extractelement, llvm.shufflevector over 1-D vector type is natural.

Cons:

1. llvm.insertvalue / llvm.extractvalue does not accept dynamic indices but only static ones.
2. Dynamic indexing on the non-most-minor dimension requires roundtrips to memory.
3. Special intrinsics and native instructions in LLVM operate on 1-D vectors. This is not expected to be a practical limitation thanks to a vector.cast %0: vector<4x8x16x32xf32> to vector<4x4096xf32> operation, that flattens the most minor dimensions (see the bigger picture in implications on codegen).

Flattened 1-D Vector Type ¶

Pros:

1. insertelement / extractelement / shufflevector with dynamic indexing is possible over the whole lowered n-D vector type.
2. Supports special intrinsics and native operations.

Cons:

1. Requires linearization/delinearization logic everywhere, translations are complex.
2. Hides away the real HW structure behind dynamic indexing: at the end of the day, HW vector sizes are generally fixed and multiple vectors will be needed to hold a vector that is larger than the HW.
3. Unlikely peephole optimizations will result in good code: arbitrary dynamic accesses, especially at HW vector boundaries unlikely to result in regular patterns.

Discussion ¶

HW Vectors and Implications on the SW and the Programming Model ¶

As of today, the LLVM model only support 1-D vector types. This is unsurprising because historically, the vast majority of HW only supports 1-D vector registers. We note that multiple HW vendors are in the process of evolving to higher-dimensional physical vectors.

In the following discussion, let’s assume the HW vector size is 1-D and the SW vector size is n-D, with n >= 1. The same discussion would apply with 2-D HW vector size and n >= 2. In this context, most HW exhibit a vector register file. The number of such vectors is fixed. Depending on the rank and sizes of the SW vector abstraction and the HW vector sizes and number of registers, an n-D SW vector type may be materialized by a mix of multiple 1-D HW vector registers + memory locations at a given point in time.

The implication of the physical HW constraints on the programming model are that one cannot index dynamically across hardware registers: a register file can generally not be indexed dynamically. This is because the register number is fixed and one either needs to unroll explicitly to obtain fixed register numbers or go through memory. This is a constraint familiar to CUDA programmers: when declaring a private float a[4]; and subsequently indexing with a dynamic value results in so-called local memory usage (i.e. roundtripping to memory).

Implication on codegen ¶

MLIR n-D vector types are currently represented as (n-1)-D arrays of 1-D vectors when lowered to LLVM. This introduces the consequences on static vs dynamic indexing discussed previously: extractelement, insertelement and shufflevector on n-D vectors in MLIR only support static indices. Dynamic indices are only supported on the most minor 1-D vector but not the outer (n-1)-D. For other cases, explicit load / stores are required.

The implications on codegen are as follows:

1. Loops around vector values are indirect addressing of vector values, they must operate on explicit load / store operations over n-D vector types.
2. Once an n-D vector type is loaded into an SSA value (that may or may not live in n registers, with or without spilling, when eventually lowered), it may be unrolled to smaller k-D vector types and operations that correspond to the HW. This level of MLIR codegen is related to register allocation and spilling that occur much later in the LLVM pipeline.
3. HW may support >1-D vectors with intrinsics for indirect addressing within these vectors. These can be targeted thanks to explicit vector_cast operations from MLIR k-D vector types and operations to LLVM 1-D vectors + intrinsics.

Alternatively, we argue that directly lowering to a linearized abstraction hides away the codegen complexities related to memory accesses by giving a false impression of magical dynamic indexing across registers. Instead we prefer to make those very explicit in MLIR and allow codegen to explore tradeoffs. Different HW will require different tradeoffs in the sizes involved in steps 1., 2. and 3.

Decisions made at the MLIR level will have implications at a much later stage in LLVM (after register allocation). We do not envision to expose concerns related to modeling of register allocation and spilling to MLIR explicitly. Instead, each target will expose a set of “good” target operations and n-D vector types, associated with costs that PatterRewriters at the MLIR level will be able to target. Such costs at the MLIR level will be abstract and used for ranking, not for accurate performance modeling. In the future such costs will be learned.

Implication on Lowering to Accelerators ¶

To target accelerators that support higher dimensional vectors natively, we can start from either 1-D or n-D vectors in MLIR and use vector.cast to flatten the most minor dimensions to 1-D vector<Kxf32> where K is an appropriate constant. Then, the existing lowering to LLVM-IR immediately applies, with extensions for accelerator-specific intrinsics.

It is the role of an Accelerator-specific vector dialect (see codegen flow in the figure above) to lower the vector.cast. Accelerator -> LLVM lowering would then consist of a bunch of Accelerator -> Accelerator rewrites to perform the casts composed with Accelerator -> LLVM conversions + intrinsics that operate on 1-D vector<Kxf32>.

Some of those rewrites may need extra handling, especially if a reduction is involved. For example, vector.cast %0: vector<K1x...xKnxf32> to vector<Kxf32> when K != K1 * … * Kn and some arbitrary irregular vector.cast %0: vector<4x4x17xf32> to vector<Kxf32> may introduce masking and intra-vector shuffling that may not be worthwhile or even feasible, i.e. infinite cost.

However vector.cast %0: vector<K1x...xKnxf32> to vector<Kxf32> when K = K1 * … * Kn should be close to a noop.

As we start building accelerator-specific abstractions, we hope to achieve retargetable codegen: the same infra is used for CPU, GPU and accelerators with extra MLIR patterns and costs.

Implication on calling external functions that operate on vectors ¶

It is possible (likely) that we additionally need to linearize when calling an external function.

Relationship to LLVM matrix type proposal. ¶

The LLVM matrix proposal was formulated 1 year ago but seemed to be somewhat stalled until recently. In its current form, it is limited to 2-D matrix types and operations are implemented with LLVM intrinsics. In contrast, MLIR sits at a higher level of abstraction and allows the lowering of generic operations on generic n-D vector types from MLIR to aggregates of 1-D LLVM vectors. In the future, it could make sense to lower to the LLVM matrix abstraction also for CPU even though MLIR will continue needing higher level abstractions.

On the other hand, one should note that as MLIR is moving to LLVM, this document could become the unifying abstraction that people should target for 1-D vectors and the LLVM matrix proposal can be viewed as a subset of this work.

Conclusion ¶

The flattened 1-D vector design in the LLVM matrix proposal is good in a HW-specific world with special intrinsics. This is a good abstraction for register allocation, Instruction-Level-Parallelism and SoftWare-Pipelining/Modulo Scheduling optimizations at the register level. However MLIR codegen operates at a higher level of abstraction where we want to target operations on coarser-grained vectors than the HW size and on which unroll-and-jam is applied and patterns across multiple HW vectors can be matched.

This makes “nested aggregate type of 1-D vector” an appealing abstraction for lowering from MLIR because:

1. it does not hide complexity related to the buffer vs value semantics and the memory subsystem and
2. it does not rely on LLVM to magically make all the things work from a too low-level abstraction.

The use of special intrinsics in a 1-D LLVM world is still available thanks to an explicit vector.cast op.

Operations ¶

source

vector.vscale (vector::VectorScaleOp) ¶

Load vector scale size

Syntax:

operation ::= `vector.vscale` attr-dict

The vscale op returns the scale of the scalable vectors, a positive integer value that is constant at runtime but unknown at compile-time. The scale of the vector indicates the multiplicity of the vectors and vector operations. For example, a vector<[4]xi32> is equivalent to vscale consecutive vector<4xi32>; and an operation on a vector<[4]xi32> is equivalent to performing that operation vscale times, once on each <4xi32> segment of the scalable vector. The vscale op can be used to calculate the step in vector-length agnostic (VLA) loops. Right now we only support one contiguous set of scalable dimensions, all of them grouped and scaled with the value returned by ‘vscale’.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface), OpAsmOpInterface

Effects: MemoryEffects::Effect{}

Results: ¶

vector.bitcast (vector::BitCastOp) ¶

Bitcast casts between vectors

Syntax:

operation ::= `vector.bitcast` $source attr-dict `:` type($source) `to` type($result)

The bitcast operation casts between vectors of the same rank, the minor 1-D vector size is casted to a vector with a different element type but same bitwidth. In case of 0-D vectors, the bitwidth of element types must be equal.

Example:

// Example casting to a smaller element type.
%1 = vector.bitcast %0 : vector<5x1x4x3xf32> to vector<5x1x4x6xi16>

// Example casting to a bigger element type.
%3 = vector.bitcast %2 : vector<10x12x8xi8> to vector<10x12x2xi32>

// Example casting to an element type of the same size.
%5 = vector.bitcast %4 : vector<5x1x4x3xf32> to vector<5x1x4x3xi32>

// Example casting of 0-D vectors.
%7 = vector.bitcast %6 : vector<f32> to vector<i32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands: ¶

Results: ¶

vector.broadcast (vector::BroadcastOp) ¶

Broadcast operation

Syntax:

operation ::= `vector.broadcast` $source attr-dict `:` type($source) `to` type($vector)

Broadcasts the scalar or k-D vector value in the source operand to a n-D result vector such that the broadcast makes sense, i.e., the source operand is duplicated to match the given rank and sizes in the result vector. The legality rules are:

• the source operand must have the same element type as the result type
• a k-D vector <s_1 x .. x s_k x type> can be broadcast to a n-D vector <t_1 x .. x t_n x type> if
  • k <= n, and
  • the sizes in the trailing dimensions n-k < i <= n with j=i+k-n match exactly as s_j = t_i or s_j = 1:

      t_1 x   ..  t_n-k x t_n-k+1 x .. x t_i x .. x t_n
                          s_1     x .. x s_j x .. x s_k
          <duplication>         <potential stretch>
  

  • in addition, any scalable unit dimension, [1], must match exactly.

The source operand is duplicated over all the missing leading dimensions and stretched over the trailing dimensions where the source has a non-equal dimension of 1. These rules imply that any scalar broadcast (k=0) to any shaped vector with the same element type is always legal.

Example:

%0 = arith.constant 0.0 : f32
%1 = vector.broadcast %0 : f32 to vector<16xf32>
%2 = vector.broadcast %1 : vector<16xf32> to vector<4x16xf32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferIntRangeInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands: ¶

Results: ¶

vector.compressstore (vector::CompressStoreOp) ¶

Writes elements selectively from a vector as defined by a mask

Syntax:

operation ::= `vector.compressstore` $base `[` $indices `]` `,` $mask `,` $valueToStore attr-dict `:` type($base) `,` type($mask) `,` type($valueToStore)

The compress store operation writes elements from a vector into memory as defined by a base with indices and a mask vector. Compression only applies to the innermost dimension. When the mask is set, the corresponding element from the vector is written next to memory. Otherwise, no action is taken for the element. Informally the semantics are:

index = i
if (mask[0]) base[index++] = value[0]
if (mask[1]) base[index++] = value[1]
etc.

Note that the index increment is done conditionally.

If a mask bit is set and the corresponding index is out-of-bounds for the given base, the behavior is undefined. If a mask bit is not set, no value is stored regardless of the index, and the index is allowed to be out-of-bounds.

The compress store can be used directly where applicable, or can be used during progressively lowering to bring other memory operations closer to hardware ISA support for a compress. The semantics of the operation closely correspond to those of the llvm.masked.compressstore intrinsic.

Examples:

vector.compressstore %base[%i], %mask, %value
  : memref<?xf32>, vector<8xi1>, vector<8xf32>

vector.compressstore %base[%i, %j], %mask, %value
  : memref<?x?xf32>, vector<16xi1>, vector<16xf32>

Operands: ¶

vector.constant_mask (vector::ConstantMaskOp) ¶

Creates a constant vector mask

Syntax:

operation ::= `vector.constant_mask` $mask_dim_sizes attr-dict `:` type(results)

Creates and returns a vector mask where elements of the result vector are set to ‘0’ or ‘1’, based on whether the element indices are contained within a hyper-rectangular region specified by the ‘mask_dim_sizes’ array attribute argument. Each element of the ‘mask_dim_sizes’ array, specifies an exclusive upper bound [0, mask-dim-size-element-value) for a unique dimension in the vector result. The conjunction of the ranges define a hyper-rectangular region within which elements values are set to 1 (otherwise element values are set to 0). Each value of ‘mask_dim_sizes’ must be non-negative and not greater than the size of the corresponding vector dimension (as opposed to vector.create_mask which allows this). Sizes that correspond to scalable dimensions are implicitly multiplied by vscale, though currently only zero (none set) or the size of the dim/vscale (all set) are supported.

Example:

// create a constant vector mask of size 4x3xi1 with elements in range
// 0 <= row <= 2 and 0 <= col <= 1 are set to 1 (others to 0).
%1 = vector.constant_mask [3, 2] : vector<4x3xi1>

print %1
              columns
            0    1    2
          |------------
        0 | 1    1    0
  rows  1 | 1    1    0
        2 | 1    1    0
        3 | 0    0    0

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes: ¶

Results: ¶

vector.contract (vector::ContractionOp) ¶

Vector contraction operation

Computes the sum of products of vector elements along contracting dimension pairs from 2 vectors of rank M and N respectively, adds this intermediate result to the accumulator argument of rank K, and returns a vector result of rank K (where K = num_lhs_free_dims + num_rhs_free_dims + num_batch_dims (see dimension type descriptions below)). For K = 0 (no free or batch dimensions), the accumulator and output are a scalar.

If operands and the result have types of different bitwidths, operands are promoted to have the same bitwidth as the result before performing the contraction. For integer types, only signless integer types are supported, and the promotion happens via sign extension.

An iterator type attribute list must be specified, where each element of the list represents an iterator with one of the following types:

• “reduction”: reduction dimensions are present in the lhs and rhs arguments but not in the output (and accumulator argument). These are the dimensions along which the vector contraction op computes the sum of products, and contracting dimension pair dimension sizes must match between lhs/rhs.

• “parallel”: Batch dimensions are iterator type “parallel”, and are non-contracting dimensions present in the lhs, rhs and output. The lhs/rhs co-iterate along the batch dimensions, which should be expressed in their indexing maps.

  Free dimensions are iterator type “parallel”, and are non-contraction, non-batch dimensions accessed by either the lhs or rhs (but not both). The lhs and rhs free dimensions are unrelated to each other and do not co-iterate, which should be expressed in their indexing maps.

An indexing map attribute list must be specified with an entry for lhs, rhs and acc arguments. An indexing map attribute specifies a mapping from each iterator in the iterator type list, to each dimension of an N-D vector.

An optional kind attribute may be used to specify the combining function between the intermediate result and accumulator argument of rank K. This attribute can take the values add/mul/minsi/minui/maxsi/maxui /and/or/xor for integers, and add/mul/minnumf/maxnumf /minimumf/maximumf for floats. The default is add.

Example:

// Simple DOT product (K = 0).
#contraction_accesses = [
 affine_map<(i) -> (i)>,
 affine_map<(i) -> (i)>,
 affine_map<(i) -> ()>
]
#contraction_trait = {
  indexing_maps = #contraction_accesses,
  iterator_types = ["reduction"]
}
%3 = vector.contract #contraction_trait %0, %1, %2
  : vector<10xf32>, vector<10xf32> into f32

// 2D vector contraction with one contracting dimension (matmul, K = 2).
#contraction_accesses = [
  affine_map<(i, j, k) -> (i, k)>,
  affine_map<(i, j, k) -> (k, j)>,
  affine_map<(i, j, k) -> (i, j)>
]
#contraction_trait = {
  indexing_maps = #contraction_accesses,
  iterator_types = ["parallel", "parallel", "reduction"]
}

%3 = vector.contract #contraction_trait %0, %1, %2
  : vector<4x3xf32>, vector<3x7xf32> into vector<4x7xf32>

// 4D to 3D vector contraction with two contracting dimensions and
// one batch dimension (K = 3).
#contraction_accesses = [
  affine_map<(b0, f0, f1, c0, c1) -> (c0, b0, c1, f0)>,
  affine_map<(b0, f0, f1, c0, c1) -> (b0, c1, c0, f1)>,
  affine_map<(b0, f0, f1, c0, c1) -> (b0, f0, f1)>
]
#contraction_trait = {
  indexing_maps = #contraction_accesses,
  iterator_types = ["parallel", "parallel", "parallel",
                    "reduction", "reduction"]
}

%4 = vector.contract #contraction_trait %0, %1, %2
    : vector<7x8x16x15xf32>, vector<8x16x7x5xf32> into vector<8x15x5xf32>

// Vector contraction with mixed typed. lhs/rhs have different element
// types than accumulator/result.
%5 = vector.contract #contraction_trait %0, %1, %2
  : vector<10xf16>, vector<10xf16> into f32

// Contract with max (K = 0).
#contraction_accesses = [
 affine_map<(i) -> (i)>,
 affine_map<(i) -> (i)>,
 affine_map<(i) -> ()>
]
#contraction_trait = {
  indexing_maps = #contraction_accesses,
  iterator_types = ["reduction"],
  kind = #vector.kind<maxnumf>
}
%6 = vector.contract #contraction_trait %0, %1, %2
  : vector<10xf32>, vector<10xf32> into f32

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, MaskableOpInterface, NoMemoryEffect (MemoryEffectOpInterface), VectorUnrollOpInterface

Effects: MemoryEffects::Effect{}

Attributes: ¶

Operands: ¶

Results: ¶

vector.create_mask (vector::CreateMaskOp) ¶

Creates a vector mask

Syntax:

operation ::= `vector.create_mask` $operands attr-dict `:` type(results)

Creates and returns a vector mask where elements of the result vector are set to ‘0’ or ‘1’, based on whether the element indices are contained within a hyper-rectangular region specified by the operands. Specifically, each operand specifies a range [0, operand-value) for a unique dimension in the vector result. The conjunction of the operand ranges define a hyper-rectangular region within which elements values are set to 1 (otherwise element values are set to 0). If operand-value is negative, it is treated as if it were zero, and if it is greater than the corresponding dimension size, it is treated as if it were equal to the dimension size.

Example:

// create a vector mask of size 4x3xi1 where elements in range
// 0 <= row <= 2 and 0 <= col <= 1 are set to 1 (others to 0).
%1 = vector.create_mask %c3, %c2 : vector<4x3xi1>

print %1
              columns
            0    1    2
          |------------
        0 | 1    1    0
  rows  1 | 1    1    0
        2 | 1    1    0
        3 | 0    0    0

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands: ¶

Results: ¶

vector.deinterleave (vector::DeinterleaveOp) ¶

Constructs two vectors by deinterleaving an input vector

Syntax:

operation ::= `vector.deinterleave` $source attr-dict `:` type($source) `->` type($res1)

The deinterleave operation constructs two vectors from a single input vector. The first result vector contains the elements from even indexes of the input, and the second contains elements from odd indexes. This is the inverse of a vector.interleave operation.

Each output’s trailing dimension is half of the size of the input vector’s trailing dimension. This operation requires the input vector to have a rank > 0 and an even number of elements in its trailing dimension.

The operation supports scalable vectors.

Example:

%0, %1 = vector.deinterleave %a
           : vector<8xi8> -> vector<4xi8>
%2, %3 = vector.deinterleave %b
           : vector<2x8xi8> -> vector<2x4xi8>
%4, %5 = vector.deinterleave %c
           : vector<2x8x4xi8> -> vector<2x8x2xi8>
%6, %7 = vector.deinterleave %d
           : vector<[8]xf32> -> vector<[4]xf32>
%8, %9 = vector.deinterleave %e
           : vector<2x[6]xf64> -> vector<2x[3]xf64>
%10, %11 = vector.deinterleave %f
           : vector<2x4x[6]xf64> -> vector<2x4x[3]xf64>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands: ¶

Results: ¶

vector.expandload (vector::ExpandLoadOp) ¶

Reads elements from memory and spreads them into a vector as defined by a mask

Syntax:

operation ::= `vector.expandload` $base `[` $indices `]` `,` $mask `,` $pass_thru attr-dict `:` type($base) `,` type($mask) `,` type($pass_thru) `into` type($result)

The expand load reads elements from memory into a vector as defined by a base with indices and a mask vector. Expansion only applies to the innermost dimension. When the mask is set, the next element is read from memory. Otherwise, the corresponding element is taken from a pass-through vector. Informally the semantics are:

index = i
result[0] := if mask[0] then base[index++] else pass_thru[0]
result[1] := if mask[1] then base[index++] else pass_thru[1]
etc.

Note that the index increment is done conditionally.

If a mask bit is set and the corresponding index is out-of-bounds for the given base, the behavior is undefined. If a mask bit is not set, the value comes from the pass-through vector regardless of the index, and the index is allowed to be out-of-bounds.

The expand load can be used directly where applicable, or can be used during progressively lowering to bring other memory operations closer to hardware ISA support for an expand. The semantics of the operation closely correspond to those of the llvm.masked.expandload intrinsic.

Examples:

%0 = vector.expandload %base[%i], %mask, %pass_thru
   : memref<?xf32>, vector<8xi1>, vector<8xf32> into vector<8xf32>

%1 = vector.expandload %base[%i, %j], %mask, %pass_thru
   : memref<?x?xf32>, vector<16xi1>, vector<16xf32> into vector<16xf32>

Operands: ¶

Results: ¶

vector.extractelement (vector::ExtractElementOp) ¶

Extractelement operation

Syntax:

operation ::= `vector.extractelement` $vector `[` ($position^ `:` type($position))? `]` attr-dict `:` type($vector)

Takes a 0-D or 1-D vector and a optional dynamic index position and extracts the scalar at that position.

Note that this instruction resembles vector.extract, but is restricted to 0-D and 1-D vectors and relaxed to dynamic indices. If the vector is 0-D, the position must be std::nullopt.

It is meant to be closer to LLVM’s version: https://llvm.org/docs/LangRef.html#extractelement-instruction

Example:

%c = arith.constant 15 : i32
%1 = vector.extractelement %0[%c : i32]: vector<16xf32>
%2 = vector.extractelement %z[]: vector<f32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferIntRangeInterface, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands: ¶

Results: ¶

vector.extract (vector::ExtractOp) ¶

Extract operation

Syntax:

operation ::= `vector.extract` $vector ``
              custom<DynamicIndexList>($dynamic_position, $static_position)
              attr-dict `:` type($result) `from` type($vector)

Takes an n-D vector and a k-D position and extracts the (n-k)-D vector at the proper position. Degenerates to an element type if n-k is zero.

Dynamic indices must be greater or equal to zero and less than the size of the corresponding dimension. The result is undefined if any index is out-of-bounds.

Example:

%1 = vector.extract %0[3]: vector<8x16xf32> from vector<4x8x16xf32>
%2 = vector.extract %0[2, 1, 3]: f32 from vector<4x8x16xf32>
%3 = vector.extract %1[]: vector<f32> from vector<f32>
%4 = vector.extract %0[%a, %b, %c]: f32 from vector<4x8x16xf32>
%5 = vector.extract %0[2, %b]: vector<16xf32> from vector<4x8x16xf32>

Traits: AlwaysSpeculatableImplTrait, InferTypeOpAdaptor

Interfaces: ConditionallySpeculatable, InferIntRangeInterface, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes: ¶

Operands: ¶

Results: ¶

vector.extract_strided_slice (vector::ExtractStridedSliceOp) ¶

Extract_strided_slice operation

Syntax:

operation ::= `vector.extract_strided_slice` $vector attr-dict `:` type($vector) `to` type(results)

Takes an n-D vector, k-D offsets integer array attribute, a k-sized sizes integer array attribute, a k-sized strides integer array attribute and extracts the n-D subvector at the proper offset.

At the moment strides must contain only 1s.

Returns an n-D vector where the first k-D dimensions match the sizes attribute. The returned subvector contains the elements starting at offset offsets and ending at offsets + sizes.

Example:

%1 = vector.extract_strided_slice %0
    {offsets = [0, 2], sizes = [2, 4], strides = [1, 1]}:
  vector<4x8x16xf32> to vector<2x4x16xf32>

// TODO: Evolve to a range form syntax similar to:
%1 = vector.extract_strided_slice %0[0:2:1][2:4:1]
  vector<4x8x16xf32> to vector<2x4x16xf32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes: ¶

Operands: ¶

Results: ¶

vector.fma (vector::FMAOp) ¶

Vector fused multiply-add

Syntax:

operation ::= `vector.fma` $lhs `,` $rhs `,` $acc attr-dict `:` type($lhs)

Multiply-add expressions operate on n-D vectors and compute a fused pointwise multiply-and-accumulate: $result = $lhs * $rhs + $acc. All operands and result have the same vector type. The semantics of the operation correspond to those of the llvm.fma[intrinsic](https://llvm.org/docs/LangRef.html#int-fma). In the particular case of lowering to LLVM, this is guaranteed to lower to thellvm.fma.*` intrinsic.

Example:

%3 = vector.fma %0, %1, %2: vector<8x16xf32>

Traits: AlwaysSpeculatableImplTrait, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface), VectorUnrollOpInterface

Effects: MemoryEffects::Effect{}

Operands: ¶

Results: ¶

vector.flat_transpose (vector::FlatTransposeOp) ¶

Vector matrix transposition on flattened 1-D MLIR vectors

Syntax:

operation ::= `vector.flat_transpose` $matrix attr-dict `:` type($matrix) `->` type($res)

This is the counterpart of llvm.matrix.transpose in MLIR. It serves the purposes of more progressive lowering and localized type conversion. Higher levels typically lower matrix tranpositions into ‘vector.transpose’ operations. Subsequent rewriting rule progressively lower these operations into ‘vector.flat_transpose’ operations to bring the operations closer to the hardware ISA.

The vector.flat_transpose op treats the 1-D input matrix as a 2-D matrix with rows and columns, and returns the transposed matrix in flattened form in ‘res’.

Note, the corresponding LLVM intrinsic, @llvm.matrix.transpose.*, does not support scalable vectors. Hence, this Op is only available for fixed-width vectors. Also see:

http://llvm.org/docs/LangRef.html#llvm-matrix-transpose-intrinsic

Example:

%1 = vector.flat_transpose %0 {columns = 4 : i32, rows = 4 : i32}
   : vector<16xf32> -> vector<16xf32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes: ¶

Operands: ¶

Results: ¶

vector.from_elements (vector::FromElementsOp) ¶

Operation that defines a vector from scalar elements

Syntax:

operation ::= `vector.from_elements` $elements attr-dict `:` type($result)

This operation defines a vector from one or multiple scalar elements. The number of elements must match the number of elements in the result type. All elements must have the same type, which must match the element type of the result vector type.

elements are a flattened version of the result vector in row-major order.

Example:

// %f1
%0 = vector.from_elements %f1 : vector<f32>
// [%f1, %f2]
%1 = vector.from_elements %f1, %f2 : vector<2xf32>
// [[%f1, %f2, %f3], [%f4, %f5, %f6]]
%2 = vector.from_elements %f1, %f2, %f3, %f4, %f5, %f6 : vector<2x3xf32>
// [[[%f1, %f2]], [[%f3, %f4]], [[%f5, %f6]]]
%3 = vector.from_elements %f1, %f2, %f3, %f4, %f5, %f6 : vector<3x1x2xf32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands: ¶

Results: ¶

vector.gather (vector::GatherOp) ¶

Gathers elements from memory or ranked tensor into a vector as defined by an index vector and a mask vector

Syntax:

operation ::= `vector.gather` $base `[` $indices `]` `[` $index_vec `]` `,` $mask `,` $pass_thru attr-dict `:` type($base) `,` type($index_vec)  `,` type($mask) `,` type($pass_thru) `into` type($result)

The gather operation returns an n-D vector whose elements are either loaded from memory or ranked tensor, or taken from a pass-through vector, depending on the values of an n-D mask vector. If a mask bit is set, the corresponding result element is defined by the base with indices and the n-D index vector (each index is a 1-D offset on the base). Otherwise, the corresponding element is taken from the n-D pass-through vector. Informally the semantics are:

result[0] := if mask[0] then base[index[0]] else pass_thru[0]
result[1] := if mask[1] then base[index[1]] else pass_thru[1]
etc.

If a mask bit is set and the corresponding index is out-of-bounds for the given base, the behavior is undefined. If a mask bit is not set, the value comes from the pass-through vector regardless of the index, and the index is allowed to be out-of-bounds.

The gather operation can be used directly where applicable, or can be used during progressively lowering to bring other memory operations closer to hardware ISA support for a gather.

Examples:

%0 = vector.gather %base[%c0][%v], %mask, %pass_thru
   : memref<?xf32>, vector<2x16xi32>, vector<2x16xi1>, vector<2x16xf32> into vector<2x16xf32>

%1 = vector.gather %base[%i, %j][%v], %mask, %pass_thru
   : memref<16x16xf32>, vector<16xi32>, vector<16xi1>, vector<16xf32> into vector<16xf32>

Interfaces: MaskableOpInterface, VectorUnrollOpInterface

Operands: ¶

Results: ¶

vector.insertelement (vector::InsertElementOp) ¶

Insertelement operation

Syntax:

operation ::= `vector.insertelement` $source `,` $dest `[` ($position^ `:` type($position))? `]`  attr-dict `:`
              type($result)

Takes a scalar source, a 0-D or 1-D destination vector and a dynamic index position and inserts the source into the destination at the proper position.

Note that this instruction resembles vector.insert, but is restricted to 0-D and 1-D vectors and relaxed to dynamic indices.

It is meant to be closer to LLVM’s version: https://llvm.org/docs/LangRef.html#insertelement-instruction

Example:

%c = arith.constant 15 : i32
%f = arith.constant 0.0f : f32
%1 = vector.insertelement %f, %0[%c : i32]: vector<16xf32>
%2 = vector.insertelement %f, %z[]: vector<f32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferIntRangeInterface, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands: ¶

Results: ¶

vector.insert (vector::InsertOp) ¶

Insert operation

Syntax:

operation ::= `vector.insert` $source `,` $dest custom<DynamicIndexList>($dynamic_position, $static_position)
              attr-dict `:` type($source) `into` type($dest)

Takes an n-D source vector, an (n+k)-D destination vector and a k-D position and inserts the n-D source into the (n+k)-D destination at the proper position. Degenerates to a scalar or a 0-d vector source type when n = 0.

Dynamic indices must be greater or equal to zero and less than the size of the corresponding dimension. The result is undefined if any index is out-of-bounds.

Example:

%2 = vector.insert %0, %1[3] : vector<8x16xf32> into vector<4x8x16xf32>
%5 = vector.insert %3, %4[2, 1, 3] : f32 into vector<4x8x16xf32>
%8 = vector.insert %6, %7[] : f32 into vector<f32>
%11 = vector.insert %9, %10[%a, %b, %c] : vector<f32> into vector<4x8x16xf32>
%12 = vector.insert %4, %10[2, %b] : vector<16xf32> into vector<4x8x16xf32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferIntRangeInterface, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes: ¶

Operands: ¶

Results: ¶

vector.insert_strided_slice (vector::InsertStridedSliceOp) ¶

Strided_slice operation

Syntax:

operation ::= `vector.insert_strided_slice` $source `,` $dest attr-dict `:` type($source) `into` type($dest)

Takes a k-D source vector, an n-D destination vector (n >= k), n-sized offsets integer array attribute, a k-sized strides integer array attribute and inserts the k-D source vector as a strided subvector at the proper offset into the n-D destination vector.

At the moment strides must contain only 1s.

Returns an n-D vector that is a copy of the n-D destination vector in which the last k-D dimensions contain the k-D source vector elements strided at the proper location as specified by the offsets.

Example:

%2 = vector.insert_strided_slice %0, %1
    {offsets = [0, 0, 2], strides = [1, 1]}:
  vector<2x4xf32> into vector<16x4x8xf32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes: ¶

Operands: ¶

Results: ¶

vector.interleave (vector::InterleaveOp) ¶

Constructs a vector by interleaving two input vectors

Syntax:

operation ::= `vector.interleave` $lhs `,` $rhs  attr-dict `:` type($lhs) `->` type($result)

The interleave operation constructs a new vector by interleaving the elements from the trailing (or final) dimension of two input vectors, returning a new vector where the trailing dimension is twice the size.

Note that for the n-D case this differs from the interleaving possible with vector.shuffle, which would only operate on the leading dimension.

Another key difference is this operation supports scalable vectors, though currently a general LLVM lowering is limited to the case where only the trailing dimension is scalable.

Example:

%a = arith.constant dense<[0, 1]> : vector<2xi32>
%b = arith.constant dense<[2, 3]> : vector<2xi32>
// The value of `%0` is `[0, 2, 1, 3]`.
%0 = vector.interleave %a, %b : vector<2xi32> -> vector<4xi32>

// Examples showing allowed input and result types.
%1 = vector.interleave %c, %d : vector<f16> -> vector<2xf16>
%2 = vector.interleave %e, %f : vector<6x3xf32> -> vector<6x6xf32>
%3 = vector.interleave %g, %h : vector<[4]xi32> -> vector<[8]xi32>
%4 = vector.interleave %i, %j : vector<2x4x[2]xf64> -> vector<2x4x[4]xf64>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands: ¶

Results: ¶

vector.load (vector::LoadOp) ¶

Reads an n-D slice of memory into an n-D vector

Syntax:

operation ::= `vector.load` $base `[` $indices `]` attr-dict `:` type($base) `,` type($result)

The ‘vector.load’ operation reads an n-D slice of memory into an n-D vector. It takes a ‘base’ memref, an index for each memref dimension and a result vector type as arguments. It returns a value of the result vector type. The ‘base’ memref and indices determine the start memory address from which to read. Each index provides an offset for each memref dimension based on the element type of the memref. The shape of the result vector type determines the shape of the slice read from the start memory address. The elements along each dimension of the slice are strided by the memref strides. When loading more than 1 element, only unit strides are allowed along the most minor memref dimension. These constraints guarantee that elements read along the first dimension of the slice are contiguous in memory.

The memref element type can be a scalar or a vector type. If the memref element type is a scalar, it should match the element type of the result vector. If the memref element type is vector, it should match the result vector type.

Example: 0-D vector load on a scalar memref.

%result = vector.load %base[%i, %j] : memref<100x100xf32>, vector<f32>

Example: 1-D vector load on a scalar memref.

%result = vector.load %base[%i, %j] : memref<100x100xf32>, vector<8xf32>

Example: 1-D vector load on a vector memref.

%result = vector.load %memref[%i, %j] : memref<200x100xvector<8xf32>>, vector<8xf32>

Example: 2-D vector load on a scalar memref.

%result = vector.load %memref[%i, %j] : memref<200x100xf32>, vector<4x8xf32>

Example: 2-D vector load on a vector memref.

%result = vector.load %memref[%i, %j] : memref<200x100xvector<4x8xf32>>, vector<4x8xf32>

Representation-wise, the ‘vector.load’ operation permits out-of-bounds reads. Support and implementation of out-of-bounds vector loads is target-specific. No assumptions should be made on the value of elements loaded out of bounds. Not all targets may support out-of-bounds vector loads.

Example: Potential out-of-bound vector load.

%result = vector.load %memref[%index] : memref<?xf32>, vector<8xf32>

Example: Explicit out-of-bound vector load.

%result = vector.load %memref[%c0] : memref<7xf32>, vector<8xf32>

Attributes: ¶

Operands: ¶

Results: ¶

vector.mask (vector::MaskOp) ¶

Predicates a maskable vector operation

The vector.mask is a MaskingOpInterface operation that predicates the execution of another operation. It takes an i1 vector mask and an optional passthru vector as arguments.

A implicitly vector.yield-terminated region encloses the operation to be masked. Values used within the region are captured from above. Only one maskable operation can be masked with a vector.mask operation at a time. An operation is maskable if it implements the MaskableOpInterface. The terminator yields all results of the maskable operation to the result of this operation.

The vector mask argument holds a bit for each vector lane and determines which vector lanes should execute the maskable operation and which ones should not. The vector.mask operation returns the value produced by the masked execution of the nested operation, if any. The masked-off lanes in the result vector are taken from the corresponding lanes of the pass-thru argument, if provided, or left unmodified, otherwise.

The vector.mask operation does not prescribe how a maskable operation should be masked or how a masked operation should be lowered. Masking constraints and some semantic details are provided by each maskable operation through the MaskableOpInterface. Lowering of masked operations is implementation defined. For instance, scalarizing the masked operation or executing the operation for the masked-off lanes are valid lowerings as long as the execution of masked-off lanes does not change the observable behavior of the program.

Examples:

  %0 = vector.mask %mask { vector.reduction <add>, %a : vector<8xi32> into i32 } : vector<8xi1> -> i32

  %0 = vector.mask %mask, %passthru { arith.divsi %a, %b : vector<8xi32> } : vector<8xi1> -> vector<8xi32>

  vector.mask %mask { vector.transfer_write %val, %t0[%idx] : vector<16xf32>, memref<?xf32> } : vector<16xi1>

  vector.mask %mask { vector.transfer_write %val, %t0[%idx] : vector<16xf32>, tensor<?xf32> } : vector<16xi1> -> tensor<?xf32>

Traits: NoRegionArguments, RecursiveMemoryEffects, SingleBlockImplicitTerminator<vector::YieldOp>, SingleBlock

Interfaces: MaskingOpInterface

Operands: ¶

Results: ¶

vector.maskedload (vector::MaskedLoadOp) ¶

Loads elements from memory into a vector as defined by a mask vector

Syntax:

operation ::= `vector.maskedload` $base `[` $indices `]` `,` $mask `,` $pass_thru attr-dict `:` type($base) `,` type($mask) `,` type($pass_thru) `into` type($result)

The masked load reads elements from memory into a vector as defined by a base with indices and a mask vector. When the mask is set, the element is read from memory. Otherwise, the corresponding element is taken from a pass-through vector. Informally the semantics are:

result[0] := if mask[0] then base[i + 0] else pass_thru[0]
result[1] := if mask[1] then base[i + 1] else pass_thru[1]
etc.

If a mask bit is set and the corresponding index is out-of-bounds for the given base, the behavior is undefined. If a mask bit is not set, the value comes from the pass-through vector regardless of the index, and the index is allowed to be out-of-bounds.

The masked load can be used directly where applicable, or can be used during progressively lowering to bring other memory operations closer to hardware ISA support for a masked load. The semantics of the operation closely correspond to those of the llvm.masked.load intrinsic.

Examples:

%0 = vector.maskedload %base[%i], %mask, %pass_thru
   : memref<?xf32>, vector<8xi1>, vector<8xf32> into vector<8xf32>

%1 = vector.maskedload %base[%i, %j], %mask, %pass_thru
   : memref<?x?xf32>, vector<16xi1>, vector<16xf32> into vector<16xf32>

Operands: ¶

Results: ¶

vector.maskedstore (vector::MaskedStoreOp) ¶

Stores elements from a vector into memory as defined by a mask vector

Syntax:

operation ::= `vector.maskedstore` $base `[` $indices `]` `,` $mask `,` $valueToStore attr-dict `:` type($base) `,` type($mask) `,` type($valueToStore)

The masked store operation writes elements from a vector into memory as defined by a base with indices and a mask vector. When the mask is set, the corresponding element from the vector is written to memory. Otherwise, no action is taken for the element. Informally the semantics are:

if (mask[0]) base[i+0] = value[0]
if (mask[1]) base[i+1] = value[1]
etc.

If a mask bit is set and the corresponding index is out-of-bounds for the given base, the behavior is undefined. If a mask bit is not set, no value is stored regardless of the index, and the index is allowed to be out-of-bounds.

The masked store can be used directly where applicable, or can be used during progressively lowering to bring other memory operations closer to hardware ISA support for a masked store. The semantics of the operation closely correspond to those of the llvm.masked.store intrinsic.

Examples:

vector.maskedstore %base[%i], %mask, %value
  : memref<?xf32>, vector<8xi1>, vector<8xf32>

vector.maskedstore %base[%i, %j], %mask, %value
  : memref<?x?xf32>, vector<16xi1>, vector<16xf32>

Operands: ¶

vector.matrix_multiply (vector::MatmulOp) ¶

Vector matrix multiplication op that operates on flattened 1-D MLIR vectors

Syntax:

operation ::= `vector.matrix_multiply` $lhs `,` $rhs attr-dict `:` `(` type($lhs) `,` type($rhs) `)` `->` type($res)

This is the counterpart of llvm.matrix.multiply in MLIR. It serves the purposes of more progressive lowering and localized type conversion. Higher levels typically lower matrix multiplications into ‘vector.contract’ operations. Subsequent rewriting rule progressively lower these operations into ‘vector.matrix_multiply’ operations to bring the operations closer to the hardware ISA.

The ‘vector.matrix_multiply’ op treats lhs as matrix with <lhs_rows> rows and <lhs_columns> columns, rhs as matrix with <lhs_columns> rows and <rhs_columns> and multiplies them. The result matrix is returned embedded in the result vector.

Note, the corresponding LLVM intrinsic, @llvm.matrix.multiply.*, does not support scalable vectors. Hence, this Op is only available for fixed-width vectors. Also see:

http://llvm.org/docs/LangRef.html#llvm-matrix-multiply-intrinsic

Example:

%C = vector.matrix_multiply %A, %B
  { lhs_rows = 4: i32, lhs_columns = 16: i32 , rhs_columns = 3: i32 } :
  (vector<64xf64>, vector<48xf64>) -> vector<12xf64>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes: ¶

Operands: ¶

Results: ¶

vector.multi_reduction (vector::MultiDimReductionOp) ¶

Multi-dimensional reduction operation

Syntax:

operation ::= `vector.multi_reduction` $kind `,` $source `,` $acc attr-dict $reduction_dims `:` type($source) `to` type($dest)

Reduces an n-D vector into an (n-k)-D vector (or a scalar when k == n) using the given operation: add/mul/minsi/minui/maxsi/maxui /and/or/xor for integers, and add/mul/minnumf/maxnumf/minimumf /maximumf for floats. Takes an initial accumulator operand.

Example:

%1 = vector.multi_reduction <add>, %0, %acc0 [1, 3] :
  vector<4x8x16x32xf32> to vector<4x16xf32>
%2 = vector.multi_reduction <add>, %1, %acc1 [0, 1] :
  vector<4x16xf32> to f32

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, MaskableOpInterface, NoMemoryEffect (MemoryEffectOpInterface), VectorUnrollOpInterface

Effects: MemoryEffects::Effect{}

Attributes: ¶

Operands: ¶

Results: ¶

vector.outerproduct (vector::OuterProductOp) ¶

Vector outerproduct with optional fused add

Takes 2 1-D vectors and returns the 2-D vector containing the outer-product, as illustrated below:

 outer |   [c, d]
 ------+------------
   [a, | [ [a*c, a*d],
    b] |   [b*c, b*d] ]

This operation also accepts a 1-D vector lhs and a scalar rhs. In this case a simple AXPY operation is performed, which returns a 1-D vector.

    [a, b] * c = [a*c, b*c]

An optional extra vector argument with the same shape as the output vector may be specified in which case the operation returns the sum of the outer-product and the extra vector. In this multiply-accumulate scenario for floating-point arguments, the rounding mode is enforced by guaranteeing that a fused-multiply add operation is emitted. When lowered to the LLVMIR dialect, this form emits llvm.intr.fma, which is guaranteed to lower to actual fma instructions on x86.

An optional kind attribute may be specified to be: add/mul/minsi /minui/maxsi/maxui/and/or/xor for integers, and add/mul /minnumf/maxnumf/minimumf/maximumf for floats. The default is add.

Example:

%2 = vector.outerproduct %0, %1: vector<4xf32>, vector<8xf32>
return %2: vector<4x8xf32>

%3 = vector.outerproduct %0, %1, %2:
  vector<4xf32>, vector<8xf32>, vector<4x8xf32>
return %3: vector<4x8xf32>

%4 = vector.outerproduct %0, %1, %2 {kind = #vector.kind<maxnumf>}:
  vector<4xf32>, vector<8xf32>, vector<4x8xf32>
return %3: vector<4x8xf32>

%6 = vector.outerproduct %4, %5: vector<10xf32>, f32
return %6: vector<10xf32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, MaskableOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes: ¶

Operands: ¶

Results: ¶

vector.print (vector::PrintOp) ¶

Print operation (for testing and debugging)

Syntax:

operation ::= `vector.print` ($source^ `:` type($source))?
              oilist(
              `str` $stringLiteral
              | `punctuation` $punctuation)
              attr-dict

Prints the source vector (or scalar) to stdout in a human-readable format (for testing and debugging). No return value.

Example:

%v = arith.constant dense<0.0> : vector<4xf32>
vector.print %v : vector<4xf32>

When lowered to LLVM, the vector print is decomposed into elementary printing method calls that at runtime will yield:

( 0.0, 0.0, 0.0, 0.0 )

This is printed to stdout via a small runtime support library, which only needs to provide a few printing methods (single value for all data types, opening/closing bracket, comma, newline).

By default vector.print adds a newline after the vector, but this can be controlled by the punctuation attribute. For example, to print a comma after instead do:

vector.print %v : vector<4xf32> punctuation <comma>

Note that it is possible to use the punctuation attribute alone. The following will print a single newline:

vector.print punctuation <newline>

Additionally, to aid with debugging and testing vector.print can also print constant strings:

vector.print str "Hello, World!"

Interfaces: MemoryEffectOpInterface (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{MemoryEffects::Write on ::mlir::SideEffects::DefaultResource}

Attributes: ¶

Syntax:
string-attribute ::= string-literal (`:` type)?
A string attribute is an attribute that represents a string literal value.
Examples:
"An important string"
"string with a type" : !dialect.string

Operands: ¶

vector.reduction (vector::ReductionOp) ¶

Reduction operation

Syntax:

operation ::= `vector.reduction` $kind `,` $vector (`,` $acc^)? (`fastmath` `` $fastmath^)? attr-dict `:` type($vector) `into` type($dest)

Reduces an 1-D vector “horizontally” into a scalar using the given operation: add/mul/minsi/minui/maxsi/maxui/and/or/xor for integers, and add/mul/minnumf/maxnumf/minimumf/maximumf for floats. Reductions also allow an optional fused accumulator.

Note that these operations are restricted to 1-D vectors to remain close to the corresponding LLVM intrinsics:

http://llvm.org/docs/LangRef.html#vector-reduction-intrinsics

Example:

%1 = vector.reduction <add>, %0 : vector<16xf32> into f32

%3 = vector.reduction <xor>, %2 : vector<4xi32> into i32

%4 = vector.reduction <mul>, %0, %1 : vector<16xf32> into f32

Traits: AlwaysSpeculatableImplTrait

Interfaces: ArithFastMathInterface, ConditionallySpeculatable, MaskableOpInterface, NoMemoryEffect (MemoryEffectOpInterface), VectorUnrollOpInterface

Effects: MemoryEffects::Effect{}

Attributes: ¶

Operands: ¶

Results: ¶

vector.scalable.extract (vector::ScalableExtractOp) ¶

Extract subvector from scalable vector operation

Syntax:

operation ::= `vector.scalable.extract` $source `[` $pos `]` attr-dict `:` type($res) `from` type($source)

Takes rank-1 source vector and a position pos within the source vector, and extracts a subvector starting from that position.

The extraction position must be a multiple of the minimum size of the result vector. For the operation to be well defined, the destination vector must fit within the source vector from the specified position. Since the source vector is scalable and its runtime length is unknown, the validity of the operation can’t be verified nor guaranteed at compile time.

Example:

%1 = vector.scalable.extract %0[8] : vector<4xf32> from vector<[8]xf32>
%3 = vector.scalable.extract %2[0] : vector<[4]xf32> from vector<[8]xf32>

Invalid example:

%1 = vector.scalable.extract %0[5] : vector<4xf32> from vector<[16]xf32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes: ¶

Operands: ¶

Results: ¶

vector.scalable.insert (vector::ScalableInsertOp) ¶

Insert subvector into scalable vector operation

Syntax:

operation ::= `vector.scalable.insert` $source `,` $dest `[` $pos `]` attr-dict `:` type($source) `into` type($dest)

This operations takes a rank-1 fixed-length or scalable subvector and inserts it within the destination scalable vector starting from the position specificed by pos. If the source vector is scalable, the insertion position will be scaled by the runtime scaling factor of the source subvector.

The insertion position must be a multiple of the minimum size of the source vector. For the operation to be well defined, the source vector must fit in the destination vector from the specified position. Since the destination vector is scalable and its runtime length is unknown, the validity of the operation can’t be verified nor guaranteed at compile time.

Example:

%2 = vector.scalable.insert %0, %1[8] : vector<4xf32> into vector<[16]xf32>
%5 = vector.scalable.insert %3, %4[0] : vector<8xf32> into vector<[4]xf32>
%8 = vector.scalable.insert %6, %7[0] : vector<[4]xf32> into vector<[8]xf32>

Invalid example:

%2 = vector.scalable.insert %0, %1[5] : vector<4xf32> into vector<[16]xf32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes: ¶

Operands: ¶

Results: ¶

vector.scan (vector::ScanOp) ¶

Scan operation

Syntax:

operation ::= `vector.scan` $kind `,` $source `,` $initial_value attr-dict `:` type($source) `,` type($initial_value)

Performs an inclusive/exclusive scan on an n-D vector along a single dimension returning an n-D result vector using the given operation (add/mul/minsi/minui/maxsi/maxui/and/or/xor for integers, and add/mul/minnumf/maxnumf/minimumf/maximumf for floats), and a specified value for the initial value. The operator returns the result of scan as well as the result of the last reduction in the scan.

Example:

%1:2 = vector.scan <add>, %0, %acc {inclusive = false, reduction_dim = 1 : i64} :
  vector<4x8x16x32xf32>, vector<4x16x32xf32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes: ¶

Operands: ¶

Results: ¶

vector.scatter (vector::ScatterOp) ¶

Scatters elements from a vector into memory as defined by an index vector and a mask vector

Syntax:

operation ::= `vector.scatter` $base `[` $indices `]` `[` $index_vec `]` `,` $mask `,` $valueToStore attr-dict `:` type($base) `,` type($index_vec)  `,` type($mask) `,` type($valueToStore)

The scatter operation stores elements from a 1-D vector into memory as defined by a base with indices and an additional 1-D index vector, but only if the corresponding bit in a 1-D mask vector is set. Otherwise, no action is taken for that element. Informally the semantics are:

if (mask[0]) base[index[0]] = value[0]
if (mask[1]) base[index[1]] = value[1]
etc.

If a mask bit is set and the corresponding index is out-of-bounds for the given base, the behavior is undefined. If a mask bit is not set, no value is stored regardless of the index, and the index is allowed to be out-of-bounds.

If the index vector contains two or more duplicate indices, the behavior is undefined. Underlying implementation may enforce strict sequential semantics. TODO: always enforce strict sequential semantics?

The scatter operation can be used directly where applicable, or can be used during progressively lowering to bring other memory operations closer to hardware ISA support for a scatter. The semantics of the operation closely correspond to those of the llvm.masked.scatter intrinsic.

Examples:

vector.scatter %base[%c0][%v], %mask, %value
    : memref<?xf32>, vector<16xi32>, vector<16xi1>, vector<16xf32>

vector.scatter %base[%i, %j][%v], %mask, %value
    : memref<16x16xf32>, vector<16xi32>, vector<16xi1>, vector<16xf32>

Operands: ¶

vector.shape_cast (vector::ShapeCastOp) ¶

Shape_cast casts between vector shapes

Syntax:

operation ::= `vector.shape_cast` $source attr-dict `:` type($source) `to` type($result)

The shape_cast operation casts between an n-D source vector shape and a k-D result vector shape (the element type remains the same).

If reducing rank (n > k), result dimension sizes must be a product of contiguous source dimension sizes. If expanding rank (n < k), source dimensions must factor into a contiguous sequence of destination dimension sizes. Each source dim is expanded (or contiguous sequence of source dims combined) in source dimension list order (i.e. 0 <= i < n), to produce a contiguous sequence of result dims (or a single result dim), in result dimension list order (i.e. 0 <= j < k). The product of all source dimension sizes and all result dimension sizes must match.

It is currently assumed that this operation does not require moving data, and that it will be folded away before lowering vector operations.

There is an exception to the folding expectation when targeting llvm.intr.matrix operations. We need a type conversion back and forth from a 2-D MLIR vector to a 1-D flattened LLVM vector.shape_cast lowering to LLVM is supported in that particular case, for now.

Example:

// Example casting to a lower vector rank.
%1 = vector.shape_cast %0 : vector<5x1x4x3xf32> to vector<20x3xf32>

// Example casting to a higher vector rank.
%3 = vector.shape_cast %2 : vector<10x12x8xf32> to vector<5x2x3x4x8xf32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferIntRangeInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands: ¶

Results: ¶

vector.shuffle (vector::ShuffleOp) ¶

Shuffle operation

Syntax:

operation ::= `vector.shuffle` operands $mask attr-dict `:` type(operands)

The shuffle operation constructs a permutation (or duplication) of elements from two input vectors, returning a vector with the same element type as the input and a length that is the same as the shuffle mask. The two input vectors must have the same element type, same rank , and trailing dimension sizes and shuffles their values in the leading dimension (which may differ in size) according to the given mask. The legality rules are:

• the two operands must have the same element type as the result
  • Either, the two operands and the result must have the same rank and trailing dimension sizes, viz. given two k-D operands v1 : <s_1 x s_2 x .. x s_k x type> and v2 : <t_1 x t_2 x .. x t_k x type> we have s_i = t_i for all 1 < i <= k
  • Or, the two operands must be 0-D vectors and the result is a 1-D vector.
• the mask length equals the leading dimension size of the result
• numbering the input vector indices left to right across the operands, all mask values must be within range, viz. given two k-D operands v1 and v2 above, all mask values are in the range [0,s_1+t_1)

Note, scalable vectors are not supported.

Example:

%0 = vector.shuffle %a, %b[0, 3]
           : vector<2xf32>, vector<2xf32>       ; yields vector<2xf32>
%1 = vector.shuffle %c, %b[0, 1, 2]
           : vector<2x16xf32>, vector<1x16xf32> ; yields vector<3x16xf32>
%2 = vector.shuffle %a, %b[3, 2, 1, 0]
           : vector<2xf32>, vector<2xf32>       ; yields vector<4xf32>
%3 = vector.shuffle %a, %b[0, 1]
           : vector<f32>, vector<f32>           ; yields vector<2xf32>

Traits: AlwaysSpeculatableImplTrait, InferTypeOpAdaptor

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes: ¶

Operands: ¶

Results: ¶

vector.splat (vector::SplatOp) ¶

Vector splat or broadcast operation

Syntax:

operation ::= `vector.splat` $input attr-dict `:` type($aggregate)

Broadcast the operand to all elements of the result vector. The operand is required to be of integer/index/float type.

Example:

%s = arith.constant 10.1 : f32
%t = vector.splat %s : vector<8x16xf32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferIntRangeInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands: ¶

Results: ¶

vector.step (vector::StepOp) ¶

A linear sequence of values from 0 to N

Syntax:

operation ::= `vector.step` attr-dict `:` type($result)

A step operation produces an index vector, i.e. a 1-D vector of values of index type that represents a linear sequence from 0 to N-1, where N is the number of elements in the result vector.

Supports fixed-width and scalable vectors.

Examples:

%0 = vector.step : vector<4xindex> ; [0, 1, 2, 3]
%1 = vector.step : vector<[4]xindex> ; [0, 1, .., <vscale * 4 - 1>]

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Results: ¶

vector.store (vector::StoreOp) ¶

Writes an n-D vector to an n-D slice of memory

Syntax:

operation ::= `vector.store` $valueToStore `,` $base `[` $indices `]` attr-dict `:` type($base) `,` type($valueToStore)

The ‘vector.store’ operation writes an n-D vector to an n-D slice of memory. It takes the vector value to be stored, a ‘base’ memref and an index for each memref dimension. The ‘base’ memref and indices determine the start memory address from which to write. Each index provides an offset for each memref dimension based on the element type of the memref. The shape of the vector value to store determines the shape of the slice written from the start memory address. The elements along each dimension of the slice are strided by the memref strides. When storing more than 1 element, only unit strides are allowed along the most minor memref dimension. These constraints guarantee that elements written along the first dimension of the slice are contiguous in memory.

The memref element type can be a scalar or a vector type. If the memref element type is a scalar, it should match the element type of the value to store. If the memref element type is vector, it should match the type of the value to store.

Example: 0-D vector store on a scalar memref.

vector.store %valueToStore, %memref[%i, %j] : memref<200x100xf32>, vector<f32>

Example: 1-D vector store on a scalar memref.

vector.store %valueToStore, %memref[%i, %j] : memref<200x100xf32>, vector<8xf32>

Example: 1-D vector store on a vector memref.

vector.store %valueToStore, %memref[%i, %j] : memref<200x100xvector<8xf32>>, vector<8xf32>

Example: 2-D vector store on a scalar memref.

vector.store %valueToStore, %memref[%i, %j] : memref<200x100xf32>, vector<4x8xf32>

Example: 2-D vector store on a vector memref.

vector.store %valueToStore, %memref[%i, %j] : memref<200x100xvector<4x8xf32>>, vector<4x8xf32>

Representation-wise, the ‘vector.store’ operation permits out-of-bounds writes. Support and implementation of out-of-bounds vector stores are target-specific. No assumptions should be made on the memory written out of bounds. Not all targets may support out-of-bounds vector stores.

Example: Potential out-of-bounds vector store.

vector.store %valueToStore, %memref[%index] : memref<?xf32>, vector<8xf32>

Example: Explicit out-of-bounds vector store.

vector.store %valueToStore, %memref[%c0] : memref<7xf32>, vector<8xf32>

Attributes: ¶

Operands: ¶

vector.transfer_read (vector::TransferReadOp) ¶

Reads a supervector from memory into an SSA vector value.

The vector.transfer_read op performs a read from a slice within a MemRef or a Ranked Tensor supplied as its first operand into a vector of the same base elemental type.

A memref/tensor operand with vector element type, must have its vector element type match a suffix (shape and element type) of the vector (e.g. memref<3x2x6x4x3xf32>, vector<1x1x4x3xf32>).

The slice is further defined by a full-rank index within the MemRef/Tensor, supplied as the operands [1 .. 1 + rank(memref/tensor)) that defines the starting point of the transfer (e.g. %A[%i0, %i1, %i2]).

The permutation_map attribute is an affine-map which specifies the transposition on the slice to match the vector shape. The permutation map may be implicit and omitted from parsing and printing if it is the canonical minor identity map (i.e. if it does not permute or broadcast any dimension).

The size of the slice is specified by the size of the vector, given as the return type.

An SSA value padding of the same elemental type as the MemRef/Tensor is provided to specify a fallback value in the case of out-of-bounds accesses and/or masking.

An optional SSA value mask may be specified to mask out elements read from the MemRef/Tensor. The mask type is an i1 vector with a shape that matches how elements are read from the MemRef/Tensor, before any permutation or broadcasting. Elements whose corresponding mask element is 0 are masked out and replaced with padding.

For every vector dimension, the boolean array attribute in_bounds specifies if the transfer is guaranteed to be within the source bounds. If set to “false”, accesses (including the starting point) may run out-of-bounds along the respective vector dimension as the index increases. Non-vector dimensions must always be in-bounds. The in_bounds array length has to be equal to the vector rank. This attribute has a default value: false (i.e. “out-of-bounds”). When skipped in the textual IR, the default value is assumed. Similarly, the OP printer will omit this attribute when all dimensions are out-of-bounds (i.e. the default value is used).

A vector.transfer_read can be lowered to a simple load if all dimensions are specified to be within bounds and no mask was specified.

This operation is called ‘read’ by opposition to ’load’ because the super-vector granularity is generally not representable with a single hardware register. A vector.transfer_read is thus a mid-level abstraction that supports super-vectorization with non-effecting padding for full-tile only operations.

More precisely, let’s dive deeper into the permutation_map for the following MLIR:

vector.transfer_read %A[%expr1, %expr2, %expr3, %expr4]
  { permutation_map : (d0,d1,d2,d3) -> (d2,0,d0) } :
  memref<?x?x?x?xf32>, vector<3x4x5xf32>

This operation always reads a slice starting at %A[%expr1, %expr2, %expr3, %expr4]. The size of the slice can be inferred from the resulting vector shape and walking back through the permutation map: 3 along d2 and 5 along d0, so the slice is: %A[%expr1 : %expr1 + 5, %expr2, %expr3:%expr3 + 3, %expr4]

That slice needs to be read into a vector<3x4x5xf32>. Since the permutation map is not full rank, there must be a broadcast along vector dimension 1.

A notional lowering of vector.transfer_read could generate code resembling:

// %expr1, %expr2, %expr3, %expr4 defined before this point
// alloc a temporary buffer for performing the "gather" of the slice.
%tmp = memref.alloc() : memref<vector<3x4x5xf32>>
for %i = 0 to 3 {
  affine.for %j = 0 to 4 {
    affine.for %k = 0 to 5 {
      // Note that this load does not involve %j.
      %a = load %A[%expr1 + %k, %expr2, %expr3 + %i, %expr4] : memref<?x?x?x?xf32>
      // Update the temporary gathered slice with the individual element
      %slice = memref.load %tmp : memref<vector<3x4x5xf32>> -> vector<3x4x5xf32>
      %updated = vector.insert %a, %slice[%i, %j, %k] : f32 into vector<3x4x5xf32>
      memref.store %updated, %tmp : memref<vector<3x4x5xf32>>
}}}
// At this point we gathered the elements from the original
// memref into the desired vector layout, stored in the `%tmp` allocation.
%vec = memref.load %tmp : memref<vector<3x4x5xf32>> -> vector<3x4x5xf32>

On a GPU one could then map i, j, k to blocks and threads. Notice that the temporary storage footprint could conceptually be only 3 * 5 values but 3 * 4 * 5 values are actually transferred between %A and %tmp.

Alternatively, if a notional vector broadcast operation were available, we could avoid the loop on %j and the lowered code would resemble:

// %expr1, %expr2, %expr3, %expr4 defined before this point
%tmp = memref.alloc() : memref<vector<3x4x5xf32>>
for %i = 0 to 3 {
  affine.for %k = 0 to 5 {
    %a = load %A[%expr1 + %k, %expr2, %expr3 + %i, %expr4] : memref<?x?x?x?xf32>
    %slice = memref.load %tmp : memref<vector<3x4x5xf32>> -> vector<3x4x5xf32>
    // Here we only store to the first element in dimension one
    %updated = vector.insert %a, %slice[%i, 0, %k] : f32 into vector<3x4x5xf32>
    memref.store %updated, %tmp : memref<vector<3x4x5xf32>>
}}
// At this point we gathered the elements from the original
// memref into the desired vector layout, stored in the `%tmp` allocation.
// However we haven't replicated them alongside the first dimension, we need
// to broadcast now.
%partialVec = load %tmp : memref<vector<3x4x5xf32>> -> vector<3x4x5xf32>
%vec = broadcast %tmpvec, 1 : vector<3x4x5xf32>

where broadcast broadcasts from element 0 to all others along the specified dimension. This time, the number of loaded element is 3 * 5 values. An additional 1 broadcast is required. On a GPU this broadcast could be implemented using a warp-shuffle if loop j were mapped to threadIdx.x.

Syntax

operation ::= ssa-id `=` `vector.transfer_read` ssa-use-list
  `{` attribute-entry `} :` memref-type `,` vector-type

Example:

// Read the slice `%A[%i0, %i1:%i1+256, %i2:%i2+32]` into vector<32x256xf32>
// and pad with %f0 to handle the boundary case:
%f0 = arith.constant 0.0f : f32
affine.for %i0 = 0 to %0 {
  affine.for %i1 = 0 to %1 step 256 {
    affine.for %i2 = 0 to %2 step 32 {
      %v = vector.transfer_read %A[%i0, %i1, %i2], (%f0)
           {permutation_map: (d0, d1, d2) -> (d2, d1)} :
           memref<?x?x?xf32>, vector<32x256xf32>
}}}

// or equivalently (rewrite with vector.transpose)
%f0 = arith.constant 0.0f : f32
affine.for %i0 = 0 to %0 {
  affine.for %i1 = 0 to %1 step 256 {
    affine.for %i2 = 0 to %2 step 32 {
      %v0 = vector.transfer_read %A[%i0, %i1, %i2], (%f0)
           {permutation_map: (d0, d1, d2) -> (d1, d2)} :
           memref<?x?x?xf32>, vector<256x32xf32>
      %v = vector.transpose %v0, [1, 0] :
          vector<256x32xf32> to vector<32x256f32>
}}}

// Read the slice `%A[%i0, %i1]` (i.e. the element `%A[%i0, %i1]`) into
// vector<128xf32>. The underlying implementation will require a 1-D vector
// broadcast:
affine.for %i0 = 0 to %0 {
  affine.for %i1 = 0 to %1 {
    %3 = vector.transfer_read %A[%i0, %i1]
         {permutation_map: (d0, d1) -> (0)} :
         memref<?x?xf32>, vector<128xf32>
  }
}

// Read from a memref with vector element type.
%4 = vector.transfer_read %arg1[%c3, %c3], %vf0
  {permutation_map = (d0, d1)->(d0, d1)}
    : memref<?x?xvector<4x3xf32>>, vector<1x1x4x3xf32>

// Read from a tensor with vector element type.
%4 = vector.transfer_read %arg1[%c3, %c3], %vf0
  {permutation_map = (d0, d1)->(d0, d1)}
    : tensor<?x?xvector<4x3xf32>>, vector<1x1x4x3xf32>

// Special encoding for 0-d transfer with 0-d tensor/memref, vector shape
// {1} and permutation_map () -> (0).
%0 = vector.transfer_read %arg0[], %f0 {permutation_map = affine_map<()->(0)>} :
  tensor<f32>, vector<1xf32>

Traits: AttrSizedOperandSegments

Interfaces: ConditionallySpeculatable, DestinationStyleOpInterface, MaskableOpInterface, MemoryEffectOpInterface, VectorTransferOpInterface, VectorUnrollOpInterface

Attributes: ¶

Operands: ¶

Results: ¶

vector.transfer_write (vector::TransferWriteOp) ¶

The vector.transfer_write op writes a supervector to memory.

The vector.transfer_write op performs a write from a vector, supplied as its first operand, into a slice within a MemRef or a Ranked Tensor of the same base elemental type, supplied as its second operand.

A vector memref/tensor operand must have its vector element type match a suffix (shape and element type) of the vector (e.g. memref<3x2x6x4x3xf32>, vector<1x1x4x3xf32>). If the operand is a tensor, the operation returns a new tensor of the same type.

The slice is further defined by a full-rank index within the MemRef/Tensor, supplied as the operands [2 .. 2 + rank(memref/tensor)) that defines the starting point of the transfer (e.g. %A[%i0, %i1, %i2, %i3]).

The permutation_map attribute is an affine-map which specifies the transposition on the slice to match the vector shape. The permutation map may be implicit and omitted from parsing and printing if it is the canonical minor identity map (i.e. if it does not permute any dimension). In contrast to transfer_read, write ops cannot have broadcast dimensions.

The size of the slice is specified by the size of the vector.

An optional SSA value mask may be specified to mask out elements written to the MemRef/Tensor. The mask type is an i1 vector with a shape that matches how elements are written into the MemRef/Tensor, after applying any permutation. Elements whose corresponding mask element is 0 are masked out.

For every vector dimension, the boolean array attribute in_bounds specifies if the transfer is guaranteed to be within the source bounds. If set to “false”, accesses (including the starting point) may run out-of-bounds along the respective vector dimension as the index increases. Non-vector dimensions must always be in-bounds. The in_bounds array length has to be equal to the vector rank. This attribute has a default value: false (i.e. “out-of-bounds”). When skipped in the textual IR, the default value is assumed. Similarly, the OP printer will omit this attribute when all dimensions are out-of-bounds (i.e. the default value is used).

A vector.transfer_write can be lowered to a simple store if all dimensions are specified to be within bounds and no mask was specified.

This operation is called ‘write’ by opposition to ‘store’ because the super-vector granularity is generally not representable with a single hardware register. A vector.transfer_write is thus a mid-level abstraction that supports super-vectorization with non-effecting padding for full-tile-only code. It is the responsibility of vector.transfer_write’s implementation to ensure the memory writes are valid. Different lowerings may be pertinent depending on the hardware support.

Example:

// write vector<16x32x64xf32> into the slice
//   `%A[%i0, %i1:%i1+32, %i2:%i2+64, %i3:%i3+16]`:
for %i0 = 0 to %0 {
  affine.for %i1 = 0 to %1 step 32 {
    affine.for %i2 = 0 to %2 step 64 {
      affine.for %i3 = 0 to %3 step 16 {
        %val = `ssa-value` : vector<16x32x64xf32>
        vector.transfer_write %val, %A[%i0, %i1, %i2, %i3]
          {permutation_map: (d0, d1, d2, d3) -> (d3, d1, d2)} :
          vector<16x32x64xf32>, memref<?x?x?x?xf32>
}}}}

// or equivalently (rewrite with vector.transpose)
for %i0 = 0 to %0 {
  affine.for %i1 = 0 to %1 step 32 {
    affine.for %i2 = 0 to %2 step 64 {
      affine.for %i3 = 0 to %3 step 16 {
        %val = `ssa-value` : vector<16x32x64xf32>
        %valt = vector.transpose %val, [1, 2, 0] :
              vector<16x32x64xf32> -> vector<32x64x16xf32>
        vector.transfer_write %valt, %A[%i0, %i1, %i2, %i3]
          {permutation_map: (d0, d1, d2, d3) -> (d1, d2, d3)} :
          vector<32x64x16xf32>, memref<?x?x?x?xf32>
}}}}

// write to a memref with vector element type.
vector.transfer_write %4, %arg1[%c3, %c3]
  {permutation_map = (d0, d1)->(d0, d1)}
    : vector<1x1x4x3xf32>, memref<?x?xvector<4x3xf32>>

// return a tensor where the vector is inserted into the source tensor.
%5 = vector.transfer_write %4, %arg1[%c3, %c3]
  {permutation_map = (d0, d1)->(d0, d1)}
    : vector<1x1x4x3xf32>, tensor<?x?xvector<4x3xf32>>

// Special encoding for 0-d transfer with 0-d tensor/memref, vector shape
// {1} and permutation_map () -> (0).
%1 = vector.transfer_write %0, %arg0[] {permutation_map = affine_map<()->(0)>} :
  vector<1xf32>, tensor<f32>

Traits: AttrSizedOperandSegments

Interfaces: ConditionallySpeculatable, DestinationStyleOpInterface, MaskableOpInterface, MemoryEffectOpInterface, VectorTransferOpInterface, VectorUnrollOpInterface

Attributes: ¶

Operands: ¶

Results: ¶

vector.transpose (vector::TransposeOp) ¶

Vector transpose operation

Syntax:

operation ::= `vector.transpose` $vector `,` $permutation attr-dict `:` type($vector) `to` type($result)

Takes a n-D vector and returns the transposed n-D vector defined by the permutation of ranks in the n-sized integer array attribute (in case of 0-D vectors the array attribute must be empty).

In the operation

%1 = vector.transpose %0, [i_1, .., i_n]
  : vector<d_1 x .. x d_n x f32>
  to vector<d_trans[0] x .. x d_trans[n-1] x f32>

the permutation array [i_1, .., i_n] must be a permutation of [0, .., n-1].

Example:

%1 = vector.transpose %0, [1, 0] : vector<2x3xf32> to vector<3x2xf32>

 [ [a, b, c],       [ [a, d],
   [d, e, f] ]  ->    [b, e],
                      [c, f] ]

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface), VectorUnrollOpInterface

Effects: MemoryEffects::Effect{}

Attributes: ¶

Operands: ¶

Results: ¶

vector.type_cast (vector::TypeCastOp) ¶

Type_cast op converts a scalar memref to a vector memref

Syntax:

operation ::= `vector.type_cast` $memref attr-dict `:` type($memref) `to` type($result)

Performs a conversion from a memref with scalar element to a memref with a single vector element, copying the shape of the memref to the vector. This is the minimal viable operation that is required to makeke super-vectorization operational. It can be seen as a special case of the view operation but scoped in the super-vectorization context.

Example:

%A  = memref.alloc() : memref<5x4x3xf32>
%VA = vector.type_cast %A : memref<5x4x3xf32> to memref<vector<5x4x3xf32>>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface), ViewLikeOpInterface

Effects: MemoryEffects::Effect{}

Operands: ¶

Results: ¶

vector.warp_execute_on_lane_0 (vector::WarpExecuteOnLane0Op) ¶

Executes operations in the associated region on thread #0 of aSPMD program

warp_execute_on_lane_0 is an operation used to bridge the gap between vector programming and SPMD programming model like GPU SIMT. It allows to trivially convert a region of vector code meant to run on a multiple threads into a valid SPMD region and then allows incremental transformation to distribute vector operations on the threads.

Any code present in the region would only be executed on first thread/lane based on the laneid operand. The laneid operand is an integer ID between [0, warp_size). The warp_size attribute indicates the number of lanes in a warp.

Operands are vector values distributed on all lanes that may be used by the single lane execution. The matching region argument is a vector of all the values of those lanes available to the single active lane. The distributed dimension is implicit based on the shape of the operand and argument. the properties of the distribution may be described by extra attributes (e.g. affine map).

Return values are distributed on all lanes using laneId as index. The vector is distributed based on the shape ratio between the vector type of the yield and the result type. If the shapes are the same this means the value is broadcasted to all lanes. In the future the distribution can be made more explicit using affine_maps and will support having multiple Ids.

Therefore the warp_execute_on_lane_0 operations allow to implicitly copy between lane0 and the lanes of the warp. When distributing a vector from lane0 to all the lanes, the data are distributed in a block cyclic way. For exemple vector<64xf32> gets distributed on 32 threads and map to vector<2xf32> where thread 0 contains vector[0] and vector[1].

During lowering values passed as operands and return value need to be visible to different lanes within the warp. This would usually be done by going through memory.

The region is not isolated from above. For values coming from the parent region not going through operands only the lane 0 value will be accesible so it generally only make sense for uniform values.

Example:

// Execute in parallel on all threads/lanes.
vector.warp_execute_on_lane_0 (%laneid)[32] {
  // Serial code running only on thread/lane 0.
  ...
}
// Execute in parallel on all threads/lanes.

This may be lowered to an scf.if region as below:

  // Execute in parallel on all threads/lanes.
  %cnd = arith.cmpi eq, %laneid, %c0 : index
  scf.if %cnd {
    // Serial code running only on thread/lane 0.
    ...
  }
  // Execute in parallel on all threads/lanes.

When the region has operands and/or return values:

// Execute in parallel on all threads/lanes.
%0 = vector.warp_execute_on_lane_0(%laneid)[32]
args(%v0 : vector<4xi32>) -> (vector<1xf32>) {
^bb0(%arg0 : vector<128xi32>) :
  // Serial code running only on thread/lane 0.
  ...
  vector.yield %1 : vector<32xf32>
}
// Execute in parallel on all threads/lanes.

values at the region boundary would go through memory:

// Execute in parallel on all threads/lanes.
...
// Store the data from each thread into memory and Synchronization.
%tmp0 = memreg.alloc() : memref<128xf32>
%tmp1 = memreg.alloc() : memref<32xf32>
%cnd = arith.cmpi eq, %laneid, %c0 : index
vector.store %v0, %tmp0[%laneid] : memref<128xf32>, vector<4xf32>
some_synchronization_primitive
scf.if %cnd {
  // Serialized code running only on thread 0.
  // Load the data from all the threads into a register from thread 0. This
  // allow threads 0 to access data from all the threads.
  %arg0 = vector.load %tmp0[%c0] : memref<128xf32>, vector<128xf32>
  ...
  // Store the data from thread 0 into memory.
  vector.store %1, %tmp1[%c0] : memref<32xf32>, vector<32xf32>
}
// Synchronization and load the data in a block cyclic way so that the
// vector is distributed on all threads.
some_synchronization_primitive
%0 = vector.load %tmp1[%laneid] : memref<32xf32>, vector<32xf32>
// Execute in parallel on all threads/lanes.

Traits: RecursiveMemoryEffects, SingleBlockImplicitTerminator<vector::YieldOp>, SingleBlock

Interfaces: RegionBranchOpInterface

Attributes: ¶

Operands: ¶

Results: ¶

vector.yield (vector::YieldOp) ¶

Terminates and yields values from vector regions.

Syntax:

operation ::= `vector.yield` attr-dict ($operands^ `:` type($operands))?

“vector.yield” yields an SSA value from the Vector dialect op region and terminates the regions. The semantics of how the values are yielded is defined by the parent operation. If “vector.yield” has any operands, the operands must correspond to the parent operation’s results. If the parent operation defines no value the vector.yield may be omitted when printing the region.

Traits: AlwaysSpeculatableImplTrait, ReturnLike, Terminator

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface), RegionBranchTerminatorOpInterface

Effects: MemoryEffects::Effect{}

Operands: ¶